Some Algorithms for Exponentiation: Left-to-Right Binary Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

Left-to-Right Binary Algorithm

Suppose we need to compute a²². We can do it by ﬁrst computing a¹¹ and then squaring it to give (a¹¹)² = a²². We can compute a¹¹ similarly but since 11 is odd, we can express a¹¹ = a¹⁰a, and compute a¹⁰ by ﬁrst computing a⁵ and squaring it. This recursive process can be repeated till the trivial subproblem of computing a¹. The subproblems created in this example have exponents as (in order of their creation): 11, 5, 2, 1. This gives us a recursive algorithm based on Divide-and-Conquer approach. We will now try to ﬁnd its iterative equivalent.

The binary representation of b helps us here. Depending upon whether any exponent e is even or odd, we are creating a subproblem with exponent e∕2 or (e− 1)∕2. So, if the binary form of b has m bits, the ﬁrst subproblem’s exponent consists of (m− 1) preﬁx bits of b. By repeating this argument, we know that the subproblems (in order of their creation) will have their exponent as these many preﬁx bits of b: m − 1,m − 2,m − 3,…,2,1.

To create the iterative equivalent of the recursive algorithm, we can solve the subproblems in bottom to top order; that is, solving for the exponents in this order: 1,2,3,…,m preﬁx bits of b.

In the common-structure shown earlier, x can be initialized to 1 to correspond to the single-bit preﬁx of b (the MSB, which is 1 here). Every iteration increases the number of preﬁx bits in x by 1. So, if the next bit of b to append to x is b_p, the iteration will do it by updating x to 2x + b_p. To maintain invariant P, r will be updated to (modulo n):

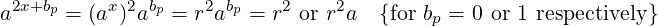The loop will terminate when x contains all the m bits of b, i.e. x = b. The following method implements this algorithm:

#define MASK_POSITION31 0x80000000

uint binary_lr(uint a, uint b, uint n)
{
  uint mask = MASK_POSITION31;
  uint r, x;

  while(!(b & mask))
    mask = mask >> 1;

  /* let p denote the position of 1-bit in the mask. */
  /* p = m-1 */
  x = 1;
  r = a % n;

  /* loop-invariants:
       X: x consists of prefix bits of b from position m-1 to p.
       P: r = (a ^ x) % n */

  while(mask != 0x1)
  {
    mask = mask >> 1; /* p decreases by 1 */

    x = x * 2; /* maintain X (step 1) */
    r = ((ulong)r * r) % n; /* maintain P */

    if(b & mask)
    {
      x = x + 1; /* maintain X (step 2) */
      r = ((ulong)r * a) % n; /* maintain P */
    }
  }
  /* x = b */

  return r;
}

As the bits from the binary representation of b are read MSB to LSB (left to right), this algorithm is often called Left-to-Right Binary Exponentiation (abbreviated as “Binary LR” algorithm below).

This algorithm performs m − 1 squarings of r, and a multiplication r ⋅ a for every 1 bit seen during the loop, which are maximum m − 1. Thus, it performs total up to 2(m − 1) multiplications, where m = ⌊log ₂b⌋ + 1.