Some Algorithms for Exponentiation: Right-to-Left Binary Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

Right-to-Left Binary Algorithm

In the above algorithm, we iteratively read the bits of b from MSB to LSB, thus building-up x from 1 to include successively more preﬁx bits of b. Alternatively, we can start with x as the single-bit suﬃx of b (the LSB), and iteratively build-up x to include successively more suﬃx bits of b. Thus, bits of b will be read from LSB to MSB (right to left). For this reason, this algorithm is often called Right-to-Left Binary Exponentiation.

In the common-structure shown earlier, every iteration increases the number of suﬃx bits in x by 1. So, if the next bit of b to prepend to x is b_p (from position p), the iteration will do it by updating x to x + b_p(2^p). To maintain invariant P, r will be updated to (modulo n):

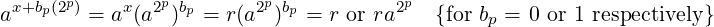A separate variable y will be maintaining the value of a^{2^p} in it as each iteration increments p by 1, starting from p = 0. The following method implements this algorithm:

uint binary_rl(uint a, uint b, uint n)
{
  uint mask, msb_mask = MASK_POSITION31;
  uint r, x, y;

  while(!(b & msb_mask))
    msb_mask = msb_mask >> 1;

  mask = 0x1;
  /* let p denote the position of 1-bit in the mask. */
  /* p = 0 */
  x = (b & mask);
  y = a % n;
  r = (x == 1 ? a % n : 1); /* x is 1 or 0 */

  /* loop-invariants:
       X: x consists of suffix bits of b from position p to 0.
       P: r = (a ^ x) % n
       Y: y = (a ^ (2^p)) % n */

  while(mask != msb_mask)
  {
    mask = mask << 1; /* p increases by 1 */

    y = ((ulong)y * y) % n; /* maintain Y */

    if(b & mask)
    {
      x = x | mask; /* effectively adding 2^p to x, to maintain X */
      r = ((ulong)r * y) % n; /* maintain P */
    }
  }
  /* x = b */

  return r;
}

This algorithm performs m − 1 squarings of y, and a multiplication r ⋅ y for every 1 bit seen during the loop, which are maximum m − 1. Thus, it performs total up to 2(m − 1) multiplications, where m = ⌊log ₂b⌋ + 1.