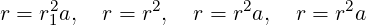
[This page is auto-generated; please prefer to read the article’s PDF Form.]
In the Binary LR algorithm, we multiply r with a whenever the bit read in an iteration is 1. Now suppose r = r1 just before an iteration. The upcoming 4 iterations will be reading 4 bits from b (assuming these many bits are left), say (1011)2, while updating r as:
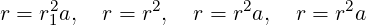 |
Thus the value of r after these 4 iterations will be: r116a11 = r124 a(1011)2. Note that this required 4 squarings of r, and 3 multiplications r ⋅a (as there are 3 1-bit in (1011)2).
In many applications of exponentiation, b may contain a large number of bits, say, in the order of 1000. Suppose, the pattern of 4 bits (1011)2 is seen again in later iterations. Then again we will be doing the above mentioned 4 squarings and 3 multiplications. But suppose we had computed a(1011)2 once and saved it somewhere. Then, whenever we find 4 consecutive bits of b being (1011)2, we can update r directly to r24 (using 4 squarings: r21 ,r22 ,r23 ,r24 ) and then to r24 a(1011)2 (using 1 multiplication with the saved value). Thus, using the precomputed value, we could reduce the number of multiplications from 4+3 to 4+1 for every occurrence of the pattern (1011)2 in b. Though, such precomputations will also be requiring certain multiplications, which we need to account for.
The 2k-ary Algorithm is based on the above idea. The bits in b are considered in groups of k (k ≥ 2) consecutive bits; the least significant k bits form a group and so on. An optimal value of k is chosen for this. Each group of k bits forms a number in range 0 to 2k − 1, and can be treated as a digit d in base 2k representation of b. The values ad are precomputed and stored in a table for each digit d in base 2k (as we will see, we need not do it for all digits). The algorithm proceeds similarly to Binary LR algorithm.
In the common-structure shown earlier, x will contain some prefix digits (in base 2k) of b at any point. It is initialized to 0 to correspond to 0 prefix digits of b. Every iteration increases the number of prefix digits in x by 1. So, if the next digit of b to append to x is d, the iteration will do it by updating x to (2k)x + d. To maintain invariant P, r can be updated to (modulo n):
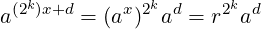 |
where ad is a precomputed value.
Now we will see how the number of values to precompute can be reduced. Any nonzero digit d in base 2k can be written:
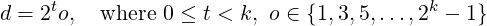 |
(t represents “power of two”, and o “odd”). We will precompute only the odd powers of a: a1,a3,a5,…,a2k−1 . In each iteration when x is updated to (2k)x + d, to maintain invariant P, r will be updated to (modulo n):
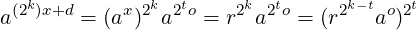 |
For this, first r2k−t will be computed using (k − t) squarings of r. Then, the precomputed ao will be multiplied with the updated r, and this result itself will be squared t times.
Note that when d is 0, we can simplify the update to r as:
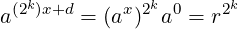 |
Following is an implementation of this algorithm:
In each iteration except the first one, this algorithm performs total k
squarings of r. The first iteration starts with r = 1, and so the first (inner) loop
of k −t squarings of r has negligible cost, leaving us with only the second loop of
t squarings of r. The total number of iterations equals the number of base 2k
digits in the m bits of b, i.e. 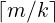 . The total squarings of r will come out to be
maximum m − 1, which is same as the m − 1 squarings of r in Binary LR
algorithm.
. The total squarings of r will come out to be
maximum m − 1, which is same as the m − 1 squarings of r in Binary LR
algorithm.
Also, each iteration does 1 multiplication r ⋅ao if d≠0. So, there will be up to
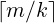 such multiplications by all iterations. The precomputation itself
involves 1 squaring (a2) and 2k−1 − 1 multiplications, hence total 2k−1
multiplications.
such multiplications by all iterations. The precomputation itself
involves 1 squaring (a2) and 2k−1 − 1 multiplications, hence total 2k−1
multiplications.
Thus, maximum total number of multiplications (including those for squaring) required is:
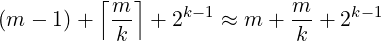 | (1) |
For a given m, let Nb and N(k) (for any integer k) denote the number of multiplications required by Binary LR algorithm and 2k-ary algorithm respectively. For k = 2, N(k) < Nb iff:

Similarly, for k = 3 and k = 4 also, when m ≤ 8, N(k) exceeds Nb. So, for the case of m ≤ 8, we can prefer Binary LR algorithm over 2k-ary algorithm. Now we will see how to choose an optimal k when m > 8.
Copyright © 2021 Nitin Verma. All rights reserved.