Some Algorithms for Exponentiation: 2k-ary Algorithm: Optimal k

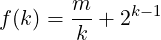
[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up]

2^k-ary Algorithm: Optimal k

We can choose the value of integer k (k ≥ 2) which minimizes the number of multiplications in (1) for a given m, which means to minimize:

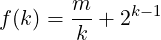m k−1 f(k) = k- + 2

For m > 8, as k increases from 0 to higher integers, f(k) ﬁrst keeps decreasing and then keeps increasing. So, to ﬁnd integer k where f(k) is minimum, we will look for the integer k at which this f(k) increase starts. More precisely, we need the smallest integer k satisfying:

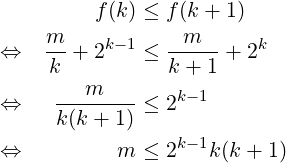
f(k) ≤ f (k + 1) m- k− 1 -m--- k ⇔ k + 2 ≤ k + 1 + 2 ---m---- k− 1 ⇔ k(k + 1) ≤ 2 k− 1 ⇔ m ≤ 2 k (k + 1)

The below table shows some ranges of m and their optimal k value:


m	9–12	13–48	49–160	161–480	481–1344	1345–3584	3585–9216

k	2	3	4	5	6	7	8

Consider some m > 8, and let k_o denote the corresponding optimal k. Then, N(k_o) must not exceed N(k) for any integer k ≥ 2. So, N(k_o) ≤ N(2). But, as seen in (2), for all m > 8, N(2) < N_b. Thus,

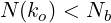N (ko) < Nb

In other words, for all m > 8, the number of multiplications required by 2^k-ary algorithm with optimally chosen k is always less than that required by Binary LR algorithm.

The number of multiplications saved by this algorithm, compared to the Binary LR algorithm, become more signiﬁcant as m increases. For example, with m = 18 and m = 52, the Binary LR algorithm requires (2(m− 1) =) 34 and 102 multiplications, but this algorithm requires (due to (1)) 18 + (18∕3) + 2² = 28 (k = 3) and 52 + (52∕4) + 2³ = 73 (k = 4) multiplications respectively.

■

[Prev] [Up]