Calculating Fibonacci Numbers: Sequential Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Sequential Algorithm

We will simply use the recurrence deﬁnition (1) of Fibonacci Numbers and sequentially calculate F₃,F₄,F₅,…,F_n. Only the two latest calculated ﬁbonacci numbers need to be remembered at any point, which will be added to obtain the next number of the sequence. Below is a portion of the C program for this. x and y remember the two latest ﬁbonacci numbers.

int i;
unsigned long x, y, z;

x = 1;
y = 1;
i = 2;

while (i < n)
{
  z = x + y;
  x = y;
  y = z;
  i = i + 1;
}

We deﬁne the Predicate P as:

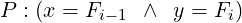P : (x = Fi−1 ∧ y = Fi)

P is true just before we enter the loop, because F₁ = F₂ = 1. It remains true after each iteration of the loop — P is the loop-invariant. So, when the loop terminates and i has become equal to n, (i = n ∧ P) holds true. Further,

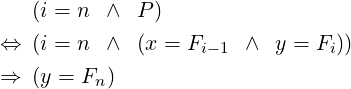
(i = n ∧ P ) ⇔ (i = n ∧ (x = Fi−1 ∧ y = Fi)) ⇒ (y = Fn)

Thus, we would receive the value of F_n in y.

This algorithm requires n− 2 iterations, doing one addition of large numbers in each iteration. Thus it performs linear (in n) number of additions on large numbers. Though, such addition itself need not have constant time-complexity.

[Prev] [Up] [Next]