Generating Permutations Lexicographically: Lexicographical Order

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Lexicographical Order

Consider two permutations of input array a:

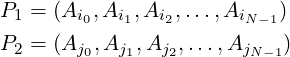
P1 = (Ai0,Ai1,Ai2,...,AiN−1) P2 = (Aj0,Aj1,Aj2,...,AjN −1)

Say, A_{i_m} is the ﬁrst element at which these two permutations diﬀer, that is A_{i_m}≠A_{j_m}. We assume that there is an order deﬁned among elements of array a, and suppose we have A_{i_m} < A_{j_m} under that order. Then we say that permutation P₁ is Lexicographically smaller than P₂. We will write P₁ < P₂.

For example, with array a = (1,2,3,4,5), the permutation (2,4,1,5,3) is smaller than (2,4,5,3,1).

Since elements of array a can be ordered, suppose we have their order as:

A < A < A < ...< A k0 k1 k2 kN−1

Then, we can reason that the following permutation is the smallest permutation in lexicographic ordering of all permutations:

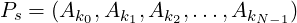Ps = (Ak0,Ak1,Ak2,...,AkN −1)

Say, any other permutation diﬀer from above permutation ﬁrst at A_{k_i}, with another element d at that position. We know that A_{k_i} is the smallest of all elements to be placed at this position onwards. So, we must have A_{k_i} < d.

And with similar reasoning, following is the largest permutation:

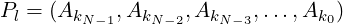P = (A ,A ,A ,...,A ) l kN−1 kN−2 kN−3 k0

[Prev] [Up] [Next]