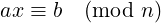
[This page is auto-generated; please prefer to read the article’s PDF Form.]
For given integers a,b,n with n > 0, a mod n≠0 and x unknown integer in ℤn, the modular linear equation looks like:
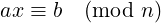 |
We need to find x, the solution of this equation where x ∈ ℤn.
This equation can also be written as: (ax−b) mod n = 0. So finding x simply means that we need to find the element in set A = {(ai − b) mod n : i ∈ ℤn} which is 0 and then the corresponding i is the desired solution x. Using Corollary 3 with its b as (−b), the set A consists of following values after taking their mod n: −b,−b + g,−b + 2g,…,−b + ((n∕g) − 1)g.
Let us assume that there exists some integer m ∈{0,1,2,…,(n∕g) − 1}, such that a value in set A, (−b + mg) mod n, is 0. Then,
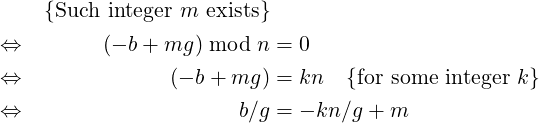
Since g∣n, if integer m exists, then b∕g must be an integer, i.e. g∣b.
On the other hand, if g∣b (b∕g is an integer), then applying Division Theorem on integer b∕g divided by integer n∕g, we know that there exist integers k and m such that 0 ≤ m < n∕g. That will be our desired m.
As m was the remainder in above division, so m = (b∕g) mod (n∕g).
Thus we have proved this in both directions: g∣b iff there exists m ∈{0,1,2,…,(n∕g) − 1} such that a value in set A, (−b + mg) mod n, is 0.
To conclude, the equation has a solution iff g∣b.
In proof of Theorem 2, we saw that the values vi = (ai) mod n are distinct for i = 0,1,2,…,t − 1 (t = n∕g), and then cycle for i = t onward as vt+j = vt. Similarly, values (ai − b) mod n will also repeat in cycles of t = n∕g distinct values.
So, if solutions of the equation exist, one solution x0 must be among {0,1,2,…,t − 1}, such that (ax0 − b) mod n = 0.
If solution x0 exists, then for every cycle of t integers i in ℤn, a solution must exist. There are g cycles, each of length t among i in ℤn. So, there will be g solutions: x = x0 + tj, j = 0,1,2,…,(n∕t) − 1.
We can write above findings in a theorem as below.
Theorem 6. For given integers a,b,n with n > 0, a mod n≠0 and g = gcd(a,n), the modular linear equation: ax ≡ b (mod n) is solvable iff g∣b. If solvable, there are total g solutions.
Corollary 7. For given integers a,b,n with n > 0, if a and n are coprime, i.e. g = gcd(a,n) = 1, then the equation ax ≡ b (mod n) has exactly one solution.
Proof. Apply Theorem 6 with g = 1. Since for all integers b, 1∣b, so the equation is solvable and has g = 1 solution. □
Corollary 8. Equation ax ≡ 1 (mod n) is solvable iff g = gcd(a,n) = 1. If solvable, it has exactly one solution.
Proof. Apply Theorem 6 with b = 1. Equation is solvable iff g∣1. That is possible only if g = 1. Such a solution is referred as the “Multiplicative Inverse of a modulo n”, and denoted as a−1 mod n. □
Proof. When n is prime, g = gcd(a,n) = 1, and so Corollary 7 applies. □
Copyright © 2020 Nitin Verma. All rights reserved.