Multiples of Golden-Ratio “Modulo” 1: Continued Fraction of ϕ

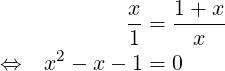
[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Continued Fraction of ϕ

We ﬁrst note that ϕ is the positive solution to the quadratic equation:

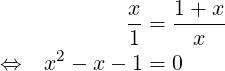
x 1 + x --= ----- 2 1 x ⇔ x − x − 1 = 0

So, ϕ = (1 + √ --
5

)∕2, and

1- ϕ = 1 + ϕ

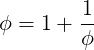Please refer to the conventions used in section “Background” of [1] about continued fractions. The continued fraction of ϕ is:

---1---- ϕ = 1 + 1+ -1--= [1;1,1,1,...] 1+...

which is special since all a_i terms are 1.

We deﬁne p₋₁ = 1 and q₋₁ = 0. For this continued fraction, we have p₀ = 1,q₀ = 1. And due to the recurrence-relation (2) in [1], for all k ≥ 0:

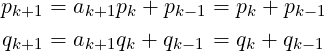
pk+1 = ak+1pk + pk−1 = pk + pk−1 qk+1 = ak+1qk + qk− 1 = qk + qk−1

Thus, for this special case of ϕ, the sequences of p_k and q_k values each follow the same recurrence-relation as the Fibonacci Sequence, which is deﬁned as:

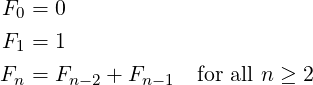
F0 = 0 F1 = 1 Fn = Fn− 2 + Fn− 1 for all n ≥ 2

So, in the continued fraction of ϕ, for all k ≥ 0:

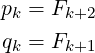
pk = Fk+2 qk = Fk+1

Thus the convergents which approximate ϕ are: p_k∕q_k = F_k+2∕F_k+1.

Now, consider any integer N ≥ 1 and its corresponding unique integers t, r and s, as deﬁned by relations (3) and (4) in [1]. The relation (3) in [1], which deﬁnes t for N, now becomes:

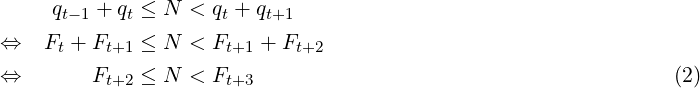
q + q ≤ N < q + q t−1 t t t+1 ⇔ Ft + Ft+1 ≤ N < Ft+1 + Ft+2 ⇔ Ft+2 ≤ N < Ft+3 (2)

So, with α = ϕ, the t ≥ 0 corresponding to N is such that F_t+2 is the largest Fibonacci number not exceeding N.

The range of r as deﬁned by relation (4) in [1] is: 1 ≤ r ≤ a_t+1. With ϕ, a_t+1 = 1 for all t ≥ 0. So in this case we have r = 1 for all N.

[Prev] [Up] [Next]