Primes in Division Method of Hashing: Division Method and Key Patterns

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Division Method and Key Patterns

In the Division Method of hashing, the hash-function h(k) is simply:

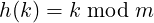h(k) = k mod m

It can be proved that, if the input keys k are randomly uniformly distributed over any set of mn consecutive integers (for some positive integer n), then their mod m values too will be uniformly distributed over ℤm = {0,1,2,…,m − 1}. That is, their hash-values h(k) will be uniformly distributed over ℤm. In this situation with input keys, m being a prime or not has no importance.

But often it is not possible to be certain that the input keys are such random. They all, or a subset of them, may exhibit some patterns. For example, a subset of input keys may follow a “linear-pattern”, where each key has the form b + ai, where a and b are ﬁxed integers and i acts as the variable integer. Such pattern can emerge due to a variety of reasons. For example:

if keys are pointers, which are all multiples of 8. Here a = 8.
if keys are all even or all odd. Here a = 2.
if keys are prices of goods most of which end at ‘9’, then a large subset of keys will be in form 9 + 10i.
consider the case when the key is formed by combining multiple components, like multiple members of an struct/object or an array. Say there are l components, each an integer: c₀,c₁,c₂,…,c_l−1. Suppose, they are multiplied by ﬁxed integers r_i to derive the integer key k as:
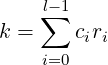$l−1 k = ∑ cr i i i=0$

Say, a group of such keys have all components in common, except one component say c_n. Then, these keys will have k in form b + (r_n)c_n, where b is ﬁxed and component c_n varies.
A common example of this is strings, where each character is a component c_i, last character being c₀. Here, 0 ≤ c_i ≤ 127 and each r_i can be chosen rⁱ, where r = 128.
Suppose a group of string keys have their last few, say n, chars common. Then every such string will have k in form b + (rⁿ)i, where b is the numeric value of the n common chars, b = ∑ _i=0ⁿ⁻¹c_irⁱ. For example, addresses often have their last part as country name, which would be common among many addresses. Similarly, email-addresses have their last part, the domain, quite common.

[Prev] [Up] [Next]