A Useful Bound from the Average

[This page is auto-generated; please prefer to read the article’s PDF Form.]

A Useful Bound from the Average

Nitin Verma

March 9, 2021

Say there are n unknown real-numbers which need not be all distinct. The only thing we know about them is their average m, and their range [l,u]. Will we be able to say anything about what proportion f(0 ≤ f ≤ 1) of these numbers are at least a given t?

The cases of t ≤ l and t > u trivially imply f = 1 and f = 0 respectively. So, we don’t really need to ﬁgure them out. Also note that, if m = l, or m = u, all n numbers must simply equal m.

There are fn numbers in this collection which are at least t. Let us refer them as bag (“multiset”) B_u (‘u’ for upper), and their sum as S_u. The remaining (1 −f)n numbers can be referred as bag B_l (‘l’ for lower), which must have sum S_l = mn − S_u.

Since all numbers are at most u:

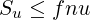Su ≤ fnu

(1)

and since numbers in bag B_u are at least t:

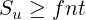S ≥ fnt u

(2)

Note that, even when bag B_u is empty (f = 0, S_u = 0), the above inequalities remain valid.

Similarly, since all numbers are at least l:

Sl ≥ (1 − f)nl ⇔ Su ≤ mn − (1− f)nl (3)

which remains valid even when bag B_l is empty: f = 1, S_l = 0.

Since numbers in bag B_l are less than t, S_l must be less than (1 −f)nt if B_l is non-empty (f < 1). For the case when B_l is empty (f = 1), we can say S_l = 0 = (1 − f)nt. So, in general:

S ≤ (1 − f)nt l ⇔ Su ≥ mn − (1− f)nt (4)

Combining (1) and (4):

fnu ≥ mn − (1− f)nt ⇔ f u ≥ m − t+ ft m − t ⇔ f ≥ -----, if t < u (5) u − t

Combining (2) and (3):

f nt ≤ mn − (1− f )nl ⇔ ft ≤ m − l + fl m − l ⇔ f ≤ -----, if t > l (6) t− l

Since l, u and m are given constants, (5) and (6) provide a relation between f and t. Note that if t ≥ m, m−t ≤ 0; so (5) provides a non-positive lower bound on f, and hence does not remain useful. Also, if t ≤ m, t − l ≤ m − l; so (6) provides an upper-bound on f which is at least 1, and hence does not remain useful.

Now, let us look at some speciﬁc cases of inequalities (5) and (6).

For t = 2m − l = m + (m − l) > m (when m > l), (6) becomes:

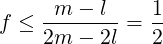f ≤ -m--−-l-= 1- 2m − 2l 2

So, at most half of the n numbers can have value of 2m − l or above.

For t = 2m − u = m − (u − m) < m (when m < u), (5) becomes:

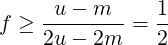-u-−-m-- 1- f ≥ 2u − 2m = 2

So, at least half of the n numbers must have value of 2m − u or above.

If all n numbers are known to be non-negative, i.e. l = 0, (6) becomes:

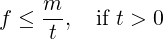f ≤ m-, if t > 0 t

which means that, for any t > 0, at most m∕t proportion of the n numbers can be t or above. This reminds us of the Markov’s Inequality.

Similarly, a corollary from the Markov’s Inequality, known as Reverse Markov’s Inequality (see, for instance [1]), corresponds to (5) above.

■

References

[1] Nick Harvey. Lecture Notes.
https://www.cs.ubc.ca/~nickhar/W12/Lecture2Notes.pdf.