Euclid’s Algorithm for GCD

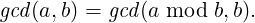[This page is auto-generated; please prefer to read the article’s PDF Form.]

The Euclid’s Algorithm for computing the gcd of two non-negative integers utilizes the following theorem.

Lemma 1. Say a and b are two non-negative integers with a ≥ b. Then, the set of Common-Divisors of (a,b) is exactly same as the set of Common-Divisors of (a mod b,b).

Proof. Say, d is a Common-Divisor of a and b. That is, d∣a and d∣b. Due to the Division Theorem, there exist unique integers q and r (denoted a mod b), 0 ≤ r < b, such that: a = qb + r = qb + a mod b.

Thus, a mod b = a−qb. Since, d∣a and d∣b, we must have, d∣(a−qb), i.e. d∣(a mod b).

So, every common-divisor of a and b must also divide a mod b, and so it is also a common-divisor of a mod b and b.

Similarly, if d′ is a common-divisor of a mod b and b, d′ must also divide qb + a mod b, which equals a. So, every common-divisor of a mod b and b is also a common-divisor of a and b. □

Due to above, the greatest integer in the set of common-divisors, the GCD, for the two pairs must also be same. Thus:

Theorem 2. Say a and b are two non-negative integers with a ≥ b. Then,

gcd(a,b) = gcd (a mod b,b).

Note that 0 ≤ a mod b < b. Also, max(a,b) = a, but max(a mod b,b) = b ≤ a. To ﬁnd the gcd of (a,b), we can try ﬁnding the gcd of smaller integer pair (a mod b,b). So, the above theorem helped us in reducing the size of the integers for which gcd is to be found.

The new pair, (a mod b,b), still consists of non-negative integers, with b > a mod b. So, we can again apply above theorem on this new pair and further reduce the size of the integers which we have to deal with. This reduction process can be repeated (until we reach a trivial case), and is what forms the basis of Euclid’s Algorithm.

Following is an implementation of this algorithm in C. The inputs A and B are any non-negative integers, and the return value is their gcd.

int euclid(const int A, const int B)
{
  int a, b;

  a = A; b = B;              /* (1) */

  while(a != 0 && b != 0)
  {
    if(a > b)
      a = a%b;               /* (2) */
    else
      b = b%a;               /* (3) */
  }

  if(a != 0)
    return a;
  else
    return b;
}