Euclid’s Algorithm for GCD: Correctness Proof

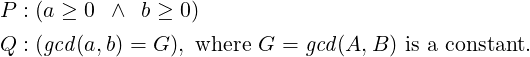
[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Correctness Proof

We will prove the correctness of Euclid’s Algorithm by arguing about the above program. We ﬁrst claim that, the invariants of its loop are:

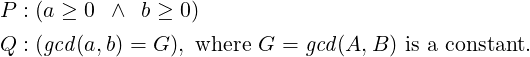
P : (a ≥ 0 ∧ b ≥ 0) Q : (gcd(a,b) = G ), where G = gcd(A,B ) is a constant.

Before the loop starts, both P and Q hold due to the assignment at point (1).

The loop’s condition is:

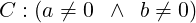C : (a ⁄= 0 ∧ b ⁄= 0)

So, whenever an iteration is entered (condition C true) with P being true, we must have:

(a > 0 ∧ b > 0)

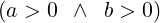The assignment (2) (or (3)) in the iteration will update a (or b) to a mod b (or b mod a), leaving it non-negative. Thus, P will continue to hold after the iteration, and so is a loop-invariant.

Additionally, the change made to a or b by an iteration does not change gcd(a,b) due to theorem 2. Thus, every iteration, though modiﬁes a or b, keeps gcd(a,b) intact. Which means, after any number of iterations, gcd(a,b) would retain its initial value, which is gcd(A,B) = G. Thus, after each iteration Q must hold, making it a loop-invariant.

Now we will prove that the loop must terminate. Consider the function t(a,b) = a + b. Before the loop starts, t(a,b) = A + B. Since the loop maintains invariant P, after each iteration t(a,b) ≥ 0. Every iteration also strictly decreases a or b, and hence t(a,b). So, t(a,b) attains only non-negative integer values, starting at A + B and strictly decreasing after each iteration. As there are only ﬁnite integers between 0 and A + B, the iterations cannot go on indeﬁnitely and must terminate.

What will have been achieved when the loop terminates? At that point, condition C must not hold, but P and Q must hold (as they do after each iteration). So, we must have:

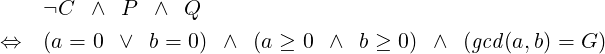
¬C ∧ P ∧ Q ⇔ (a = 0 ∨ b = 0) ∧ (a ≥ 0 ∧ b ≥ 0) ∧ (gcd (a,b) = G )

Since at least one of a and b is 0, we can assume without loss of generality, b = 0 . Then,

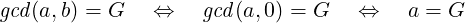gcd(a,b) = G ⇔ gcd (a,0) = G ⇔ a = G

Thus, a must contain the value of gcd(A,B). This completes the proof.

[Prev] [Up] [Next]