Extended Euclid’s Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

In an earlier article titled Euclid’s Algorithm for GCD ([1]), we have discussed the Euclid’s Algorithm for ﬁnding the GCD of two non-negative integers. In section “Bézout’s Identity”, we arrived at this well-known theorem:

Theorem 1 (Bézout’s Identity). For any non-negative integers A and B, there exist integers x,y such that:

Ax + By = gcd(A,B )

Now, we will investigate how, for a given pair (A,B), such a pair (x,y) can be found. We will frequently refer to the program and some relations established in article [1].

In section “A Generic Loop-Invariant” of [1], we deﬁned property (1) for predicates and argued that, with any such predicate R and variables a and b in the Euclid’s Algorithm program (page 2), R(a) ∧ R(b) becomes a loop-invariant.

In section “Bézout’s Identity” of [1], we introduced a predicate for non-negative integers z:

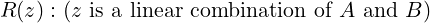and found that it satisﬁes the property (1), hence making R(a) ∧ R(b) a loop-invariant in that program. Speciﬁcally, after every iteration R(a) ∧ R(b) must hold, which means, a and b always remain a linear combination of A and B. We can express this as below, where s,t,u,v are some integers:

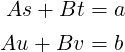
We are looking at the problem of ﬁnding integers (x,y) in the Bézout’s Identity. Notice that one of the variables a and b “incrementally” becomes the gcd(A,B) during the program. Also, during every such modiﬁcation to these variables, they still remain a linear combination of A and B. So, we can keep computing the corresponding s,t,u,v as and when a and b are modiﬁed. This would ensure that, when one of them (say, a) becomes the gcd, we must have found the desired (x,y) (as (s,t)).

Let us try modifying the Euclid’s Algorithm program in this direction. We introduce integer variables s,t,u,v and need to maintain the invariants:

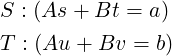
(Prof. E W Dijkstra in his EWD 1158 ([2]) used such loop-invariants to create a program so as to constructively-prove Bézout’s Identity.)

It is trivial to establish these invariants just before the loop starts (when a = A, b = B), by doing:

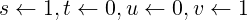Now, we need to take care of modiﬁcations to a and b which happen during the loop. Let us consider a (case of b is similar). The modiﬁcation is of the form: a ← a mod b. But a mod b = a − qb, where q = ⌊a∕b⌋ due to the Division Theorem. How can we compute the new values of s and t so as to maintain S? The new value of a, i.e. a−qb, can actually be expressed using the relations from invariants S and T as:

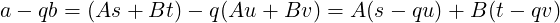So, S can be maintained by doing s ← s−qu, t ← t−qv. Similarly, whenever b is modiﬁed to b mod a = b−qa, where q = ⌊b∕a⌋, T can be maintained by doing u ← u − qs, v ← v − qt.

We have thus found a way to establish S ∧T before the loop starts and after each iteration where a or b is modiﬁed. S ∧ T is a new loop-invariant.

When the loop terminates, one of the variables a or b will contain the gcd(A,B). Suppose, a = gcd(A,B), b = 0 (the other case is similar). Then, due to loop-invariant S: As + Bt = a = gcd(A,B). So, (s,t) would be the desired integers (x,y) of Bézout’s Identity.

The modiﬁed program is shown below. This algorithm is also known as “Extended Euclid’s Algorithm”.

int euclid_extended(const int A, const int B)
{
  int a, b, s, t, u, v, q;

  a = A; b = B;
  s = 1; t = 0; u = 0; v = 1;

  while(a != 0 && b != 0)
  {
    if(a > b)
    {
      q = a/b;
      a = a - q*b;         /* same as a%b */
      s = s - q*u;
      t = t - q*v;
    }
    else
    {
      q = b/a;
      b = b - q*a;         /* same as b%a */
      u = u - q*s;
      v = v - q*t;
    }
  }

  if(a != 0)
  {
    printf("Bezout’s Identity (x,y)=(%d,%d)\n", s, t);
    return a;
  }
  else
  {
    printf("Bezout’s Identity (x,y)=(%d,%d)\n", u, v);
    return b;
  }
}

References

[1] Nitin Verma. Euclid’s Algorithm for GCD.
https://mathsanew.com/articles/euclid_algorithm_for_gcd.pdf
(2021).

[2] E W Dijkstra. A bagatelle on Euclid’s Algorithm.
https://www.cs.utexas.edu/users/EWD/ewd11xx/EWD1158.PDF
EWD 1158 (1993).