Why Some Algorithms Divide Problems Equally: Discarding of Subproblems

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up]

Discarding of Subproblems

For some kinds of problems, we may need to solve only one of the two subproblems, discarding the other one. For example, Binary-Search algorithm discards half of the array (one of the two subproblems) after each comparison. In situations where we may end up discarding some of the subproblems, the number of base-instances may be less than linear in n, and so will be the total work required. For example, Binary-Search involves O(log2(n)) work.

How do we decide the two subproblems sizes in such algorithms? Say, we want to optimize the worse case where the “costlier” of the two subproblems gets picked, discarding the other one. The costlier subproblem requires work:

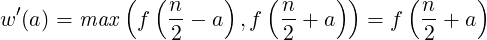( ( ) ( )) ( ) w ′(a) = max f n-− a ,f n-+ a = f n-+ a 2 2 2

Because, if f follows property (1), f(n∕2 + a) is costlier. To minimize it, we choose a = 0, i.e. the subproblems of size n∕2 each.

■

[Prev] [Up]