[This page is auto-generated; please prefer to read the article’s PDF Form.]
To be able to find n and l, this algorithm first finds out some element which belongs to the cycle. To find such element, it observes that there must exist some integer t ≥ 1 such that et and e2t are equal, i.e. have the same index. For et and e2t to be equal, they both must belong to the cycle. That is:
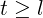 | (2) |
Let us try to find out more about such t. The index of et and e2t are same iff (due to (1)):
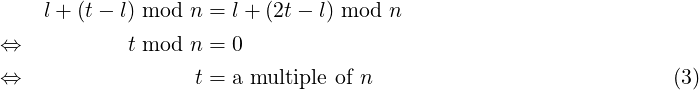
Due to (2), (3) and t ≥ 1, t is a positive multiple of n which is at least l. There are infinitely many such t, but lets try to find out the smallest of them. Now onward, we will simply use ‘t’ to denote this smallest t.
So we are looking for the smallest positive multiple of n, which is at least l. For the trivial case of l = 0, t is n. For l > 0 and n∣l, t is l.
Now consider the case of n ∤ l (which also implies l > 0). So, 0 < l mod n < n. Also, l − l mod n is a multiple of n. Hence the required t is: (l − l mod n) + n = l + n − l mod n.
For the case of l = 0 also, t = n can be written as l + n − l mod n. This reduces the number of cases we have to deal with while working with t. We can summarize our findings as:
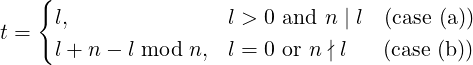 | (4) |
Notice that t ≤ l + n always. We now understand how t relates to l and n, but these quantities are still unknown. To find t and locate et, the algorithm works as follows.
It iterates over the possible values of t = 1,2,3,… while checking if the required t is reached, i.e. if et = e2t. For that, it maintains two references (pointers) R1 and R2 at et and e2t respectively, for the current t. When both R1 and R2 point to the same element et = e2t, it knows that the required t is reached.
Below is an implementation of this algorithm in C. The above described part of this method will be referred as “Cycle-Searching” (the other two parts “Find n” and “Find l” will be discussed below). Whenever a reference R is updated to f(R), we will call it one “step” taken by R.
Copyright © 2021 Nitin Verma. All rights reserved.