Cycle Detection: Floyd’s Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

Cycle Detection: Floyd’s Algorithm

Nitin Verma

August 19, 2021

Let f be a function from a ﬁnite set S to the same set. So, for any element e₀ of S, each of the elements obtained as f(e₀),f(f(e₀)),f(f(f(e₀))),… will also belong to S. For any i ≥ 0, let e_i denote the element obtained after applying function f over e₀ i times. That is,

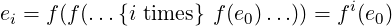i ei = f (f (...{i times } f (e0) ...)) = f (e0)

Clearly, all e_i are in S. Since S is a ﬁnite set, not all e_i can be distinct. Say, e₀,e₁,e₂,…,e_u are all distinct for some u, and e_u+1 = e_l for some l ≤ u. Due to this, e_u+2 = f(e_u+1) = f(e_l) = e_l+1, similarly e_u+3 = e_l+2, and likewise all subsequent e_i will belong to this “cycle”: e_l,e_l+1,…,e_u.

We will denote by n (n ≥ 1) the number of elements in this cycle: n = u−l + 1, and so u = l + n− 1. The following diagram depicts this situation; each arrow indicates application of function f:

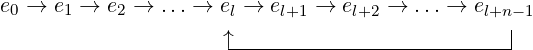
e0 → e1 → e2 → ...→ el → el+1 → el+2 → ...→ el+n −1 | ↑---------------------------

Since any e_i (including i ≥ l + n) equals one of the above l + n distinct elements, it can be associated with one particular index among these l + n elements’ indices. We will refer to it as the “index of e_i”. For i < l, the index of e_i is simply i, and for i ≥ l, the index is:

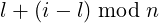l + (i− l) mod n

(1)

Given the initial element e₀ and function f, we need to ﬁnd l and n. In this article, we discuss the Floyd’s Cycle Detection Algorithm for this problem, named after R. W. Floyd ([1]: section 3.1, exercise 6). It is also called Tortoise-Hare Algorithm [2].

Many other situations can transform to this generic problem, including a well-known problem of how we can detect cycle in a linked-list (described later in section “Detecting Cycle in a Linked-List”).

[Next]