Cycle Detection: Floyd’s Algorithm: Other Step-Counts for References

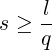
[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up]

Other Step-Counts for References

In the cycle-searching part of method ﬂoyd(), every time we progress R₁ and R₂ by 1 and 2 steps respectively. Suppose we instead progress them by p and q steps with p > q, and call the corresponding references R_p and R_q. Will these two references ever meet inside the cycle?

They will meet if there exists s ≥ 1 such that e_ps and e_qs are equal and so belong to the cycle. That is, ps ≥ l and qs ≥ l, which is equivalent to (since p > q) qs ≥ l. So:

-l s ≥ q

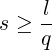(6)

Due to (1), indices of e_ps and e_qs are same iﬀ:

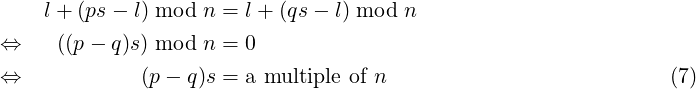
l + (ps− l) mod n = l + (qs − l) mod n ⇔ ((p− q)s) mod n = 0 ⇔ (p− q)s = a multiple of n (7)

It is in fact possible to ﬁnd s ≥ 1 which satisﬁes both (6) and (7). An example is s = mn where m is a positive integer large enough such that mn ≥ l∕q. So we can conclude that R_p and R_q will always meet after some number of iterations, for any p and q with p > q.

Note that for p = 2 and q = 1, equations (6) and (7) are equivalent to (2) and (3) respectively.

■

References

[1] D. E. Knuth. The Art of Computer Programming, Vol 2, Third Edition. Addison-Wesley (1997).

[2] Wikipedia. Cycle Detection. https://en.wikipedia.org/wiki/
Cycle_detection.

[Prev] [Up]