| 0 | 4 | 0 | 3 | 6 | |||||||
| 3 | 6 | 5 | 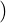 | 0 | 1 | 4 | 7 | 3 | 4 | 9 | 1 |
| 0 | |||||||||||
| 1 | 4 | 7 | 3 | ||||||||
| 1 | 4 | 6 | 0 | ||||||||
| 0 | 1 | 3 | 4 | ||||||||
| 0 | |||||||||||
| 1 | 3 | 4 | 9 | ||||||||
| 1 | 0 | 9 | 5 | ||||||||
| 2 | 5 | 4 | 1 | ||||||||
| 2 | 1 | 9 | 0 | ||||||||
| 3 | 5 | 1 |
[This page is auto-generated; please prefer to read the article’s PDF Form.]
We first look at an example of division of decimal numerals using the schoolbook algorithm, also known as Long Division Algorithm.
| 0 | 4 | 0 | 3 | 6 | |||||||
| 3 | 6 | 5 | 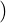 | 0 | 1 | 4 | 7 | 3 | 4 | 9 | 1 |
| 0 | |||||||||||
| 1 | 4 | 7 | 3 | ||||||||
| 1 | 4 | 6 | 0 | ||||||||
| 0 | 1 | 3 | 4 | ||||||||
| 0 | |||||||||||
| 1 | 3 | 4 | 9 | ||||||||
| 1 | 0 | 9 | 5 | ||||||||
| 2 | 5 | 4 | 1 | ||||||||
| 2 | 1 | 9 | 0 | ||||||||
| 3 | 5 | 1 |
It has been presented slightly differently. First, the dividend has been prefixed with a 0. Second, the steps which generate a digit 0 in quotient have been shown explicitly like any other step; this is so even for the initial 0 in the quotient.
Each digit of the generated quotient will be referred as a “quotient-digit”. After each subtraction, we bring down the next dividend-digit to append to the subtraction result. The value thus formed is divided by the divisor to obtain the next quotient-digit; so it is like “dividend” of a particular iteration. We will be referring such values as “Iteration’s Dividend”, abbreviated as “IDD”. In this example 1473, 0134, 1349, 2541 are all IDD of their respective iteration.
To allow us to view this algorithm as an iterative process which repeats the same kind of generic step, we can also call the initial prefix digits taken from the input dividend as an IDD. So, in this example, 0147 is also an IDD.
Note that, in this example of a 3-digit divisor, all the IDDs are up to 3 + 1 = 4 digits. Those IDDs which have less than 4 digits have been prefixed with 0s to make their width 4, e.g. 0134. In general, for a divisor b of nb digits, we will always be treating the IDDs as having width nb + 1, by prefixing some 0s if necessary. This convention will help us in our later discussion.
Note that the initial IDD always starts with a 0, followed by nb digits taken from the dividend.
Copyright © 2021 Nitin Verma. All rights reserved.