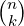= n!∕((n − k)!k!).
[This page is auto-generated; please prefer to read the article’s PDF Form.]
For a set S of n elements, a k-Combination is any of its subset having k
elements. It can be proved that, for any given k, the number of k-combinations of
S must be 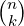= n!∕((n − k)!k!).
Given an array a of n distinct elements and a non-negative integer k (k ≤ n), suppose we need to generate all k-combinations of elements of a. In this article, we will discuss a simple recursive algorithm for the same and also write a non-recursive equivalent of that.
[Next]
Copyright © 2021 Nitin Verma. All rights reserved.