[This page is auto-generated; please prefer to read the article’s PDF Form.]
We will use ℤ to represent the set of all integers {…,−2,−1,0,1,2,…}, and ℤn to represent the set of integers {0,1,2,…,n − 1}. Below is a very fundamental theorem about division of integers.
Theorem 1 (Division Theorem). For any integers a,n with n > 0, there exist unique integers q and r such that 0 ≤ r < n and a = qn + r.
q and r are called the Quotient and Remainder of this division respectively. r is always non-negative and will be represented as a mod n. Note that, for all integers a, (a mod n) ∈ ℤn.
For any a, since r ≥ 0, we can write: a ≥ qn. So, if a < 0, then q < 0. If q < 0, then qn ≤−n. And since r < n, so if q < 0, then a = qn + r < −n + n = 0.
Thus, in brief, we can write q < 0 iff a < 0.
Note that, for any a, a mod n and (−a) mod n need not be same. For example, 3 mod 10 = 3, but (−3) mod 10 = 7.
For any integers a and b, if a mod n = b mod n, we say “a is equivalent to b modulo n”, and denote this fact as: a ≡ b (mod n). This happens iff n divides (a − b). Notice this use of the term “mod n”, which is also used as a binary operator like “a mod n”.
The case when a mod n≠b mod n, is denoted by a≢b (mod n).
It is easy to see that for all integers b such that b = a + nk for some integer k, a ≡ b (mod n).
Here are some other useful facts about the mod operation. a,b,n,i are any integers, n > 0,i ≥ 0. Please convince yourself of the reasoning behind these. Their basis is that any integer a can be expressed as a multiple of n, plus a mod n (Division Theorem).
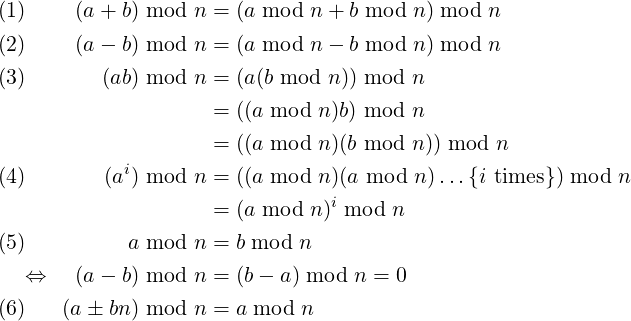
Copyright © 2020 Nitin Verma. All rights reserved.