[This page is auto-generated; please prefer to read the article’s PDF Form.]
Let α < 1 be any positive real number and N any positive integer. For any real number x, let {x} denote the fractional part of x, i.e. {x} = x −⌊x⌋. What can we say about distribution of values:
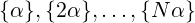 | (1) |
in the interval [0,1]? Do these values get clustered at some places or they are almost uniformly spread across [0,1]?
In this article, we will try answering the above with help of the Three Distance Theorem. The theorem is also known as the Three Gap Theorem and Steinhaus Conjecture (due to Hugo Steinhaus, who originally conjectured it).
We will often refer the values in (1) as {mα} where m is a positive integer. Whenever α is a rational number p∕q, it will be assumed that p and q are positive coprime integers and p < q.
For any real number α′ > 1 which is not an integer, we know that there exist integer n and another positive real number α < 1 such that α′ = α + n. So, for any positive integer m, {mα′} = {mα}. Hence, all values {mα′} are exactly same as values {mα} and we can restrict our analysis to α < 1.
The α being a real number can be rational or irrational. Say, α is a rational number p∕q. With the help of Modular Arithmetic (refer to Corollary 4 in article titled Multiples of an Integer Modulo Another Integer), it can be proved that, for m = 1,2,…,q, the values {mα} are all distinct and form the set: S = {0,1∕q,2∕q,…,(q − 1)∕q}.
For m = q + 1 onward, these {mα} values repeat, because for n = 1,2,3,…, {(q + n)(p∕q)} = {n(p∕q)}. So for any N ≥ q, we now know that the values in (1) form the set S and so are distributed uniformly in interval [0,1], spaced by distance 1∕q.
For any N < q, we only know that values {mα} are some subset of S of size N, but we do not know any further about their distribution. This is where the Three Distance Theorem will help us.
Now, say α is an irrational number. That is, there exist no integer p and q such that α = p∕q. Do the values {mα} repeat in this case also? Assume that they repeat and {m1α} = {m2α} for some positive integers m1 and m2 with m1 < m2. Then,
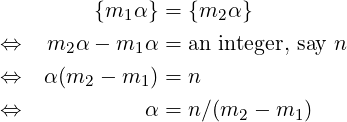
Thus we arrive at an interesting conclusion that when α is irrational, values {mα} are distinct for all positive integers m. Similarly we can prove that when α is irrational, there is no positive integer m such that {mα} = 0.
The basic statement of the Three Distance Theorem is very simple. It says that, if the values in (1) are sorted and we find the differences of all neighboring values (including interval boundaries 0 and 1), which we can call “gap lengths”, then there are either two or three distinct gap-lengths. The theorem holds for all α and N specified in (1), except that when α is rational p∕q, then it only holds for N < q.
When α = p∕q, then as discussed above, for all N ≥ q, there will be only one distinct gap-length of 1∕q. Throughout this discussion, we assume that N < q whenever α is rational p∕q.
The figure 1 below shows N = 30 points for α as rational 107∕271, as irrational ϕ− 1 (ϕ is the Golden Ratio) and irrational π − 3 (ϕ ≈ 1.6180339…,π ≈ 3.14159…). As per the theorem, for each case, there must be two or three distinct gap-lengths between neighboring points, including 0 and 1. We only took α < 1, but as noted earlier, the {mα} values will be same if we add a positive integer to the α.
There are further details in this theorem as we will see below. It also makes use of the concept of Continued Fractions. So we will first review the necessary background. The theorem’s statements and some of its details provided below are based on [1] and [2].
[Next]
Copyright © 2020 Nitin Verma. All rights reserved.