Three Distance Theorem: Background

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Background

For any positive real number α, its Simple Continued Fraction can be written as:

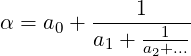----1----- α = a0 + a1 + -1--- a2+...

where for all i > 0, a_i are positive integers, and a₀ is a non-negative integer.

If α is irrational, this continued fraction never terminates, i.e. contains inﬁnitely many a_i terms, and is denoted by: [a₀;a₁,a₂,…]. For rational α, it always terminates at some term a_n, and is denoted by: [a₀;a₁,a₂,…,a_n].

For example, 25∕11 = [2;3,1,2],14∕9 = [1;1,1,4],the Golden Ratio ϕ (irrational) = [1;1,1,1,…],π (irrational) = [3;7,15,1,292,…].

We may consider only the ﬁrst few a_i terms as below and call it the k^th Convergent: p_k∕q_k = [a₀;a₁,a₂,…,a_k]. For example,

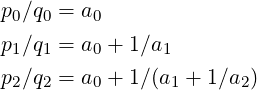
p ∕q = a 0 0 0 p1∕q1 = a0 + 1 ∕a1 p2∕q2 = a0 + 1 ∕(a1 + 1∕a2)

If we deﬁne p₋₁ = 1,q₋₁ = 0, the following recurrence relations hold for all k ≥ 0:

p = a p + p k+1 k+1 k k−1 qk+1 = ak+1qk + qk−1 (2)

It is known that p_k and q_k are coprime for all k.

The Three Distance Theorem also involves use of integer values (q_k−1 + q_k) for k ≥ 0. Note that the sequence of q_k values is: q₋₁ = 0,q₀ = 1,q₁ = a₁,q₂ = a₂a₁ + 1 etc. From (2) we also know the recurrence relation of q_k. Since a_i ≥ 1 for all i > 0, q_k are strictly increasing with k for k ≥ 1. We also see that the sequence of (q_k−1 + q_k) is strictly increasing with k for all k ≥ 0, starting at 1 for k = 0.

Hence, any integer N ≥ 1 either equals (q_k−1 + q_k) for some k ≥ 0, or is between two consecutive values of this sequence. We can conclude that, any integer N ≥ 1 corresponds to a unique integer t ≥ 0 such that:

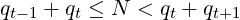qt−1 + qt ≤ N < qt + qt+1

(3)

Note that the last endpoint of this range can be written as:

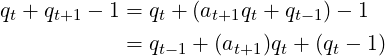
q + q − 1 = q + (a q + q )− 1 t t+1 t t+1 t t−1 = qt−1 + (at+1)qt + (qt − 1)

So, in the range of (3), (N −qt−1) varies from qt to (at+1)qt + (qt − 1). Due to the Division Theorem, given (N −qt−1) and qt, there exist unique integers r and s such that:

(N − q ) = rq + s (4) t−1 t 0 ≤ s ≤ qt − 1 {Division Theorem } 1 ≤ r ≤ at+1 {due to the range of (N − qt−1)}

Note that for a ﬁxed t, as N varies in range of (3), every increase in N by qt would increase r by 1.

Thus we now know that, any integer N ≥ 1 corresponds to unique integers t, r and s as deﬁned by (3) and (4).

Let us now move to exploring the theorem.

[Prev] [Up] [Next]