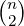 key pairs
from S. Thus, the maximum number of functions where any of these
key pairs
from S. Thus, the maximum number of functions where any of these 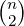 pairs
can collide is:
pairs
can collide is:
[This page is auto-generated; please prefer to read the article’s PDF Form.]
Consider a 𝜖-Universal class ℋ of H functions, mapping U to ℤm. Say we are given a set S of n keys from U. Are there any functions in ℋ which give no collision for all keys in S? We will refer to such functions as “Collision-Free” for S. So, these functions map the n distinct keys to n distinct values of ℤm. Such a function would exist only if |ℤm|≥|S|, i.e. m ≥ n.
The definition of 𝜖-Universal class provides an upper bound of 𝜖H on the
number of functions where any key pair would collide. We can form 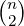 key pairs
from S. Thus, the maximum number of functions where any of these
key pairs
from S. Thus, the maximum number of functions where any of these 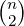 pairs
can collide is:
pairs
can collide is:
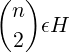 | (1) |
Note that this is only an upper-bound and can even exceed the available functions count of H. The subset of functions where a pair collides may overlap with the subset of functions where some other pair collides. Since above we simply added maximum size of each such subset (i.e. 𝜖H), once for each pair, this upper bound may be loose.
Based on (1), the minimum number of functions in ℋ which must be
collision-free for S, if  𝜖H ≤ H:
𝜖H ≤ H:
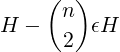 |
So, the minimum proportion of such functions in ℋ:
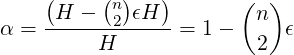 | (2) |
Although (2) need not provide a tight lower bound on the proportion of functions which are collision-free for a given set of n keys, it can still be useful. It relates the lower-bound α to 𝜖, and it may be possible to adjust the parameters of the universal class to achieve certain 𝜖. For example, for a 1∕m-Universal class, 𝜖 = 1∕m can be modified by simply modifying the table-size m.
Suppose we want to ensure the lower bound α is at least 1/2; so at least half of the functions in ℋ are collision-free for a given set of n keys. Then (2) gives:
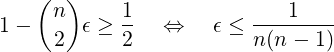 | (3) |
For any 1∕m-Universal class, (3) becomes:
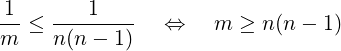 |
And for 2∕m-Universal class, (3) becomes:
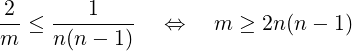 |
To make α at least f ∈ (0,1), we need:
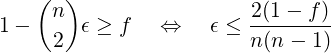 |
Theorem 1. Given 𝜖-Universal class ℋ and any set of n keys, the proportion of functions in ℋ which are collision-free for those keys is at least f ∈ (0,1) if:
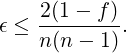 |
Corollary 2. Given 𝜖-Universal class ℋ with 𝜖 = 1∕m, and any set of n keys, at least half of the functions in ℋ are collision-free for those keys if: m ≥ n(n − 1). For 𝜖 = 2∕m, this condition is: m ≥ 2n(n − 1).
Copyright © 2021 Nitin Verma. All rights reserved.