Universal Classes of Hash Functions

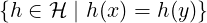
[This page is auto-generated; please prefer to read the article’s PDF Form.]

Universal Classes of Hash Functions

Nitin Verma

February 25, 2021

In this article, we will ﬁnd out how a certain proportion of hash functions in a Universal Class must have some properties.

Consider a set ℋ of hash-functions, each of which map the set of all possible keys U to {0,1,2,…,m− 1}, where m is a positive integer. ℋ is called a Universal Class if any two distinct keys x,y ∈ U map to the same value by at most |ℋ|∕m functions in ℋ. In other words, the set of functions where x and y collide:

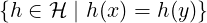{h ∈ ℋ | h (x ) = h(y)}

has at most |ℋ|∕m functions.

We will denote |ℋ| by H. For any non-negative integer i, the set {0,1,2,…,i − 1} will be denoted as ℤi, and the set {1,2,…,i − 1} as ℤi^∗.

Some set of hash-functions may demonstrate the above property for a proportion of functions which is not necessarily 1∕m. Say this proportion is 𝜖, for some real number 𝜖 in (0,1). We may call such set as 𝜖-Universal Class.

The Universal Class (without 𝜖 speciﬁed) deﬁned above has proportion 𝜖 = 1∕m, and so we will refer them as “1∕m-Universal”. In our derivation of properties, we will consider the more general 𝜖-Universal classes so that the results are more useful.

Below are two examples of 𝜖-Universal Classes. The set of all possible keys is: U = {0,1,2,…,u − 1}, for some positive integer u. p is a prime, p ≥ u.

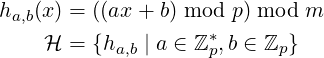
For each a ∈ ℤp^∗, b ∈ ℤp, deﬁne: $ha,b(x) = ((ax+ b) mod p) mod m ℋ = {ha,b | a ∈ ℤ∗p,b ∈ ℤp }$ ℋ is a 1∕m-Universal class.
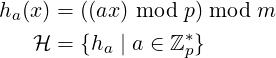
For each a ∈ ℤp^∗, deﬁne: $ha (x ) = ((ax) mod p) mod m ℋ = {ha | a ∈ ℤ∗p}$ ℋ is a 2∕m-Universal class.

Given any distinct keys x and y, these universal classes, due to their deﬁnition, carry an upper-bound on the number of their functions where x,y collide. It is this upper bound, 𝜖H, which we will utilize below to count the functions in the class with certain properties.

The kinds of relations as discussed here, were originally derived and utilized in a method of Perfect Hashing called FKS Method, by Fredman, Komlós and Szemerédi in [1]. The relations and proofs from [1] are also elaborated nicely in [2]. In these, the class of hash-functions considered is the one from example-2 above. In book [3], chapter “Hash Tables”, we ﬁnd derivation of similar relations for 1∕m-Universal Classes. The relations and proofs presented in this article are adaptation from these sources, and are for general 𝜖-Universal classes.

[Next]