Euclid’s Algorithm for GCD: Bezout’s Identity

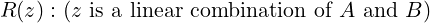
[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Bézout’s Identity

For any integers i and j, we say k is a Linear Combination of i and j if there exist integers x and y such that k = ix + jy. Say, we are given two non-negative integers A and B. Consider two integers a and b with a ≥ b > 0, each of which is a linear combination of A and B. It is easy to prove that a mod b, which is actually a − qb for some integer q (Division Theorem), must also be a linear combination of A and B.

For any non-negative integer z, let us deﬁne a predicate R as:

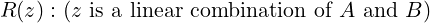R (z ) : (z is a linear combination of A and B )

Due to our observation in the last paragraph, we can say:

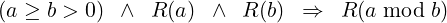(a ≥ b > 0) ∧ R(a) ∧ R (b) ⇒ R(a mod b)

So, due to theorem 3:

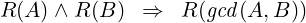R (A )∧ R (B) ⇒ R (gcd(A,B ))

Note that R(A) and R(B) hold trivially. So, R(gcd(A,B)) must also hold. That is, gcd(A,B) is a linear combination of A and B. This proves the Bézout’s Identity:

Theorem 5 (Bézout’s Identity). For any non-negative integers A and B, there exist integers x,y such that:

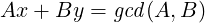Ax + By = gcd(A,B )

[Prev] [Up] [Next]