Euclid’s Algorithm for GCD: Divisors of Fibonacci Numbers

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up]

Divisors of Fibonacci Numbers

For integers i ≥ 0, say F_i denotes the i^th Fibonacci Number (F₀ = 0,F₁ = 1,F₂ = 1 etc). It is a known property about Fibonacci Numbers that, for any non-negative integers a and b with a ≥ b, and any integer d, if d∣F_a and d∣F_b, then d∣F_a−b. For a given integer d, we can deﬁne a predicate over non-negative integers x, R′(x) : (d∣F_x) . This predicate in fact satisﬁes property (2).

So, applying the corollary 4, we get, for any non-negative integers A and B:

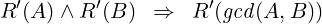′ ′ ′ R (A )∧ R (B) ⇒ R (gcd(A, B))

That means, if d∣F_A and d∣F_B, then d∣F_gcd(A,B), for any integer d.

There is a proof about Fibonacci Numbers ([1]) which did such reasoning based on Euclid’s Algorithm.

■

References

[1] Proof Wiki. GCD of Fibonacci Numbers.
https://proofwiki.org/wiki/GCD_of_Fibonacci_Numbers.

[Prev] [Up]