Symmetry in the Roots of a Quadratic Equation

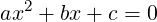
[This page is auto-generated; please prefer to read the article’s PDF Form.]

Symmetry in the Roots of a Quadratic Equation

Nitin Verma

April 8, 2021

One way to write a Quadratic Equation is:

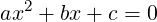2 ax + bx + c = 0

(1)

where, a,b,c are known real-numbers with a≠0, and x is an unknown number. Suppose we know one root, r₁, of this equation. Then,

2 ar 1( + br1 + c) = 0 (2) b- c- ⇔ r1 r1 + a = − a (3)

So, there are two terms on LHS, r₁ and (r₁ + b∕a), which multiply to give a constant −c∕a on RHS. Just by looking at this relation, can we know anything about another root r₂ of (1)? Finding such r₂ is equivalent to ﬁnding a number which can replace r₁ in (3). That is, the two terms r₂ and (r₂ + b∕a) must also multiply to give the same constant −c∕a.

Multiplication operation is commutative. So, one way to get the same result is to exchange the two terms being multiplied in (3), and treat (r₁ + b∕a) as r₂ and r₁ as (r₂ + b∕a). But that would require:

( ) ( ) r = r + b- = r + b+ b- ⇔ 2b = 0 2 1 a 2 a a a

which is possible only if b = 0. So this did not work. Let us try again, but this time we not only exchange the two terms but also negate each, which would still give the same result on multiplication. So, now we treat −(r₁ + b∕a) as r₂, and −r₁ as (r₂ + b∕a). This is feasible because it yields:

( ) ( ) b- b- b- r2 = − r1 + a = − − r2 − a + a = r2

Thus we have found another root r₂ = −(r₁ + b∕a). We could arrive at it by using the fact that two multiplication terms can be exchanged, and both negated, to give the same result. The relation can also be expressed as:

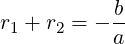b r1 + r2 = −-- a

After doing this, we may be curious to look for a way of using the commutativity of addition, like we did for multiplication (and exchange the two terms being added). We can rewrite (2) as below, assuming r₁≠0 and dividing both sides by r₁:

ar + b + c- = 0 1 r1 c b ⇔ r1 + ar- = − a- (4) 1

We now try to ﬁnd r₂ which can replace r₁ in above (again assuming r₂≠0). Note that the LHS adds two terms r₁ and c∕ar₁ to give a constant −b∕a. Can we exchange these two terms and treat c∕ar₁ as r₂, and r₁ as c∕ar₂ (for this we need c≠0, because r₁,r₂ are non-zero)? In fact this is feasible, because it yields:

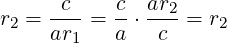c c ar2 r2 = --- = --⋅--- = r2 ar1 a c

Thus, again we could ﬁnd another root r₂ = c∕ar₁. Though, we arrived at this under some assumptions. The relation can also be expressed as:

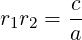r1r2 = c- a

In both of the exercises above, we could exchange the two terms being multiplied (or added) for one root, to give us the corresponding two terms for another root. This shows us a symmetry between the two roots. Another way to observe this symmetry is through the expressions r₁ + r₂ (equaling −b∕a) and r₁r₂ (equaling c∕a), where r₁ and r₂ appear in the same way and so are interchangeable.

[Next]