Symmetry in the Roots of a Quadratic Equation: Side Note

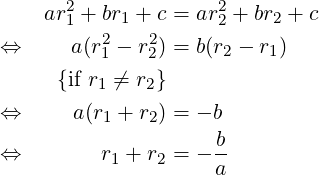
[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up]

Side Note

Above we could establish the relations about sum and product of the roots (though with some assumptions). There are other ways also to arrive at these relations. Equation (2) for r₁, and similar one for r₂, can be combined and re-arranged as:

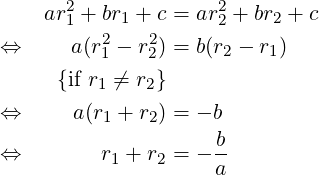
2 2 ar1 + br1 + c = ar2 + br2 + c ⇔ a(r21 − r22) = b(r2 − r1) {if r1 ⁄= r2} ⇔ a(r1 + r2) = − b b- ⇔ r1 + r2 = − a

Also, combining equation (4) for r₁ and similar one for r₂:

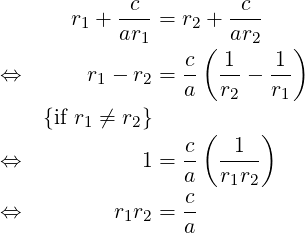
r1 + -c- = r2 + -c- ar1 ( ar2 ) ⇔ r − r = c- 1-− 1- 1 2 a r2 r1 {if r1 ⁄= r2} c ( 1 ) ⇔ 1 = -- ---- a r1r2 ⇔ r1r2 = c- a

But these derivations involved some assumptions (like r₁≠r₂), and so are not thorough. There is a complete proof of these relations based on the Factor Theorem (which itself is a consequence of the Polynomial Remainder Theorem). Due to this theorem, if r₁, r₂ are roots of (1), then, (x − r₁) and (x − r₂) are factors of the quadratic polynomial on the LHS of (1). So,

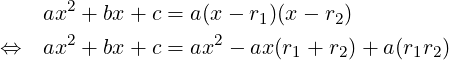
ax2 + bx + c = a(x− r )(x − r) 1 2 ⇔ ax2 + bx + c = ax2 − ax(r1 + r2)+ a(r1r2)

Equating the coeﬃcients of same powers of x of both sides, we get:

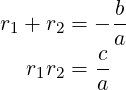
b r1 + r2 = − a c- r1r2 = a

Of course, we can also prove these relations by ﬁrst deriving the roots to be (−b ± √ -2------
b − 4ac

)∕2a, and then simplifying r₁ + r₂ and r₁r₂.

■

[Prev] [Up]