Cycle Detection: Floyd’s Algorithm: Finding l

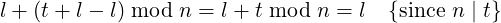
[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Finding l

We have R₁ at e_t. After l steps, it will be at index (due to (1)):

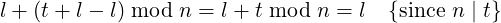l + (t+ l − l) mod n = l + t mod n = l {since n | t}

Also, say another reference R is initialized to point to e₀. It will be at index l after l steps. So, to ﬁnd l, we can iteratively step R₁ and R till they meet, while counting the steps. This step count will be l.

The above approach can be made more eﬃcient. Due to (4), (t − n) can be expressed as:

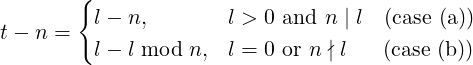{ t− n = l − n, l > 0 and n | l (case (a)) l − l mod n, l = 0 or n ∤ l (case (b ))

(5)

Clearly, 0 ≤ (t − n) ≤ l. Now consider a reference R at element e_t−n and R₁ which is already at e_t. For case (a) and (b) above, R will require n and l mod n steps respectively to reach e_l. Now consider equation (4): adding n and l mod n to t for case (a) and (b) respectively will make it l + n, and e_l+n is simply e_l (due to (1)).

Thus, for case (a), both R and R₁ after taking n steps, must point to e_l. For case (b), they must point to e_l after taking l mod n steps. So we can ﬁnd l as follows.

Initialize R at e_t−n. This can be done by stepping R from e₀ (t−n) times. R₁ is already at e_t. Now, iteratively step R and R₁ till they meet (they will meet at e_l), while counting the steps. Say, the step count comes out to be x. Adding x to (t−n) will give us the total steps taken by R to reach e_l from e₀, which must be l.

The “Find l” part in method ﬂoyd() implements this approach.

The other approach mentioned in the beginning of this section steps both R and R₁ l times. This approach steps R l times, but steps R₁ only x times where x is n (case (a)) or l mod n (case (b)).

[Prev] [Up] [Next]