Array Rotation: Dolphin Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

Array Rotation: Dolphin Algorithm

Nitin Verma

May 4, 2021

Consider an array a of n elements; the element type can be anything. Given any integer k, 1 ≤ k ≤ (n − 1), we need to right-shift this array circularly by k elements. That means, if A_i denotes the initial value of a[i] for all indices i, then elements of array a should be rearranged such that the following hold:

(∀i : 0 ≤ i < k : a[i] = An−k+i) ∧ (∀i : k ≤ i < n : a[i] = Ai−k) ⇔ (∀i : 0 ≤ i < n : a[i] = A(i− k)modn)

In words, each element of the array shifts right (to higher index) by k positions, while wrapping around the boundary at index n − 1 if required. We will refer this process as “rotating the array by k”.

Another way to look at this process is that, it interchanges the two blocks of elements which are at index ranges [0,n−k − 1] and [n−k,n− 1]; so it can also be called “block interchange”.

In this article, we will discuss the Dolphin Algorithm to perform this task, its proof and one modiﬁcation to it. The algorithm seems to be ﬁrst published in a 1966 paper by Fletcher and Silver [1], and was rediscovered and named such in [2]. Some places on internet also call it Juggling Algorithm.

Due to the rotation, if the element at index i ends up being placed at index j, we will refer such j as the “target-index” of i, and i as the “source-index” of j. Notice that the task of rotating an array is a way of rearranging its elements such that the element at index i gets moved to the target-index given by function f(i) = (i + k) mod n. We can also say that, an index i receives the element from source-index given by function g(i) = (i − k) mod n.

Now, consider the below sequence of indices in which each index is followed by its target-index:

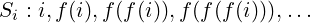Si : i,f (i),f(f(i)),f (f (f (i))),...

(1)

Since f can only take up to n values, this sequence must start repeating at some point. Note that the (j + 1)^th element (j ≥ 0) of this sequence is given by:

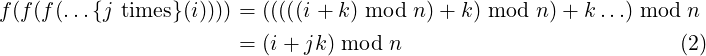
f(f(f(...{j times}(i)))) = (((((i+ k) mod n) + k) mod n)+ k...) mod n = (i+ jk) mod n (2)

The Dolphin Algorithm makes use of the nature of this sequence, which we will understand further with the help of modular arithmetic. In the next section, we prepare the relevant mathematical results.

[Next]