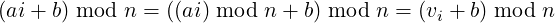
[This page is auto-generated; please prefer to read the article’s PDF Form.]
Please refer to the proof of theorem 2 in article titled Multiples of an Integer Modulo Another Integer [3]. Based on that, we can write the following theorem:
Theorem 1. For any integers a,n with n > 0, a mod n≠0, and g = gcd(a,n), denote (ai) mod n as vi for all integers i ≥ 0, and n∕g as t. Then:
Note that we did not claim anything about which value vi maps to which value in G. Further in this theorem, what can we say about values of the form (ai + b) mod n, for some integer b ≥ 0 ? Note,
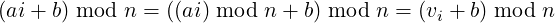 |
From theorem 1, we know that the vi values only belong to the set G. Inspecting the set G, we know that if 0 ≤ b < g, then 0 ≤ (vi + b) < n, and so:
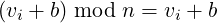 |
So, if 0 ≤ b < g, then:
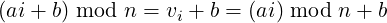 |
That is, the sequence of values (ai + b) mod n is obtained simply by adding b to each element in the sequence of values (ai) mod n. We can write the following conclusion using theorem 1:
Corollary 2. For any integers a,b,n with n > 0, 0 ≤ b < g, a mod n≠0, and g = gcd(a,n), denote (ai + b) mod n as v′i for all integers i ≥ 0, and n∕g as t. Then:
The symbols of a,n,i,j,g used in above theorems have been chosen to match those in the referred proof of [3]; they do not correspond to other objects of this article.
Copyright © 2021 Nitin Verma. All rights reserved.