[This page is auto-generated; please prefer to read the article’s PDF Form.]
We now move back to the discussion about sequence (1). As found in (2), the elements of sequence Si are given by (i + jk) mod n, for j = 0,1,2,…. Let g = gcd(k,n) and t = n∕g. Using corollary 2, we can conclude this about sequence Si for 0 ≤ i < g:
(a) the first t elements of the sequence are all distinct, forming the set Gi = {i,g + i,2g + i,…,((n∕g) − 1)g + i}. Also, the first element simply equals i.
(b) after the first t elements, the subsequence of these t elements keeps repeating in the sequence Si. That is, the (t + 1)th element equals 1st element (which is i), and so on.
(c) for all j ≥ 0, the (j + 1)th element is given by (jk) mod n + i. So, the (j + 1)th element of the g sequences S0,S1,…,Sg−1 are consecutive.
We will be referring to the subsequence of first t elements of each sequence Si as “cycle Ci”, which are nothing but elements of set Gi in some order. Note that, the tth/last value of Ci has its target-index as the first value of Ci; hence the name “cycle”.
Now observe that, for the g sets G0,G1,…,Gg−1:
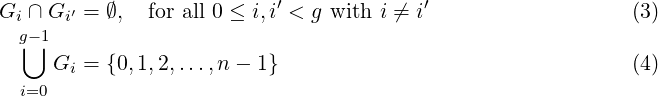
What we have so far discussed forms the mathematical basis of the Dolphin Algorithm, which we describe now. For rotating the array, that is to rearrange its n elements, the algorithm considers one cycle Ci at a time, for i = 0,1,2,…,g − 1. Recall that the cycle Ci consists of t = n∕g array indices starting with i, such that each index x is followed by its target-index f(x).
The elements of array a which are located at indices of cycle Ci, can be rearranged as required by moving them as per the cycle’s order. Now, for iterating over the cycle Ci, we can either step in the forward direction as:
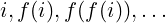 |
or backward direction as:
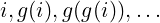 |
In the first way, a source-index is followed by its target-index. In the second one, it is the reverse. Below method implemented in C shows a way to rearrange the elements indexed by cycle Ci using the backward iteration:
Notice how the elements could be shifted along the cycle while requiring extra memory for only one array element. The forward iteration can also be implemented slightly differently.
Now, due to (3) and (4) we know that if we rearrange each of the g cycles C0,C1,…,Cg−1 as above, we will have rearranged all the n elements of the array. So, the following method must result in rotation of the array as required. For computing the gcd, it uses Euclid’s Algorithm.
Note that this algorithm moves each array element (except a[i]) only once, directly to its target-index, hence avoiding any intermediate moves. It was named “Dolphin Algorithm” by [2] because, “the movement of the array values looked like dolphins leaping out of the water and disappearing again at random places”.
Copyright © 2021 Nitin Verma. All rights reserved.