Implementing Basic Arithmetic for Large Integers: Multiplication: Multiplication by a Digit

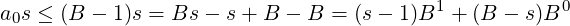
[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Multiplication by a Digit

Let us ﬁrst understand the multiplication of a by any single digit s of b. It is done iteratively by picking each digit a_i, starting at the LSD (position 0) and computing a_is. Since,

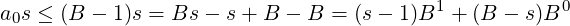a0s ≤ (B − 1)s = Bs − s+ B − B = (s− 1)B1 + (B − s)B0

so the carry produced by position 0, c₀, can be maximum (s − 1). For the computation at position 1, we have:

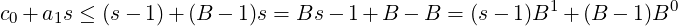1 0 c0 +a1s ≤ (s− 1)+ (B − 1)s = Bs − 1+ B − B = (s − 1 )B + (B − 1)B

So, the carry produced by position 1, c₁, also can be maximum (s− 1). Thus, by repeating such argument we know that the carry c_i produced by any position i can never exceed (s − 1).

Lemma 1. In the schoolbook multiplication algorithm, when multiplying operand a with digit s in any base B, the carry produced by any position cannot exceed (s − 1). And since s ≤ (B − 1), a carry can never exceed (B − 2).

This allows us to conclude that such a carry can be stored and added like any other digit of our base B numeral system, using the uint type.

Note that the calculation at any position i is of the form (deﬁning c₋₁ = 0): c_i−1 + a_is, which can produce values of up to 2-digit numeral in base B, because:

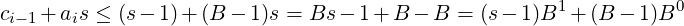1 0 ci− 1+ ais ≤ (s− 1)+ (B − 1)s = Bs − 1 +B − B = (s− 1)B + (B − 1)B

[Side Note] At all positions except the MSD position of a (i.e. i = n_a − 1), this calculation contributes the lower digit of this 2-digit value in the result (a⋅s), sending the upper digit to carry. At position i = n_a − 1, it will contribute both of its digits in the result. Now we will write a lemma which will be useful later when discussing Division operation.

Lemma 2. In the schoolbook multiplication algorithm, when multiplying operand a = (a_{n_a−1}a_{n_a−2}…a₁a₀) with digit s in any base B, the result (a⋅s) has either n_a or n_a + 1 digits. In the result, the two digits at (most-signiﬁcant) positions n_a, n_a − 1 are produced by the last iteration, which multiplies MSD of a with s. This 2-digit value is given by (c_{n_a−2} is the earlier produced carry):

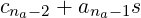cna−2 + ana−1s

[End of Side Note]

Since the calculation at any position can produce values only up to 2-digit, they should ﬁt in the “unsigned long” type.

[Prev] [Up] [Next]