Implementing Basic Arithmetic for Large Integers: Multiplication: Implementation

[This page is auto-generated; please prefer to read the article’s PDF Form.]

Implementation

Now we know how to produce each row R_i. Instead of ﬁrst producing and storing all such rows, and then adding them all (after left-shifting), we will add each row to a common result r as and when it is produced. Thus we will avoid the need to store these rows for later processing.

Below method multiply_digit() implements multiplication of a bigint by a single digit, and multiply() implements multiplication of two bigints. Please refer to [1] for implementation of methods referred by these methods.

Note that each row R_i has up to n_a + 1 digits, and after left-shifting it by i positions, it eﬀectively has n_a + i + 1 digits. When we add row R_i to the common result r, we will be performing an addition involving n_a + i + 1 digit-positions (the current r must not be having more digits than this); i.e. n_a + i + 1 iterations in the addition method. Starting with r as R₀, the addition of remaining n_b − 1 rows will require total such iterations as:

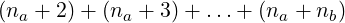So when n_a < n_b, we can reduce these iterations by swapping a and b. That is, for eﬃciency, the operand with more number of digits will always be chosen as the upper operand.

/* input struct r can also be same as struct a */
int multiply_digit(bigint *a, uint s, bigint *r)
{
  int   j;
  uint  carry = 0;
  ulong d;

  if(s == 0)
  {
    BINT_INIT(r, 0);
    return 0;
  }

  /* digits[] index j corresponds to position WIDTH-1-j in the
     positional-numeral representation */

  for(j = WIDTH-1; j >= a->msd; j--)
  {
    d = ((ulong)a->digits[j])*s + carry;
    carry = d / B;
    r->digits[j] = d % B;
  }

  if(carry)
  {
    if(j < 0)
    {
      printf("multiply_digit: overflow\n");
      return -1;
    }
    else
    {
      r->digits[j] = carry;
      r->msd = j;
    }
  }
  else
    r->msd = j + 1;

  return 0;
}

/* input r must be a separate struct than a or b */
int multiply(bigint *a, bigint *b, bigint *r)
{
  int    j;
  bigint R; /* row */

  if(BINT_LEN(a) < BINT_LEN(b))
    SWAP(a, b);

  /* digits[] index j corresponds to position WIDTH-1-j in the
     positional-numeral representation */

  multiply_digit(a, b->digits[WIDTH-1], r);

  for(j = WIDTH-2; j >= b->msd; j--)
  {
    multiply_digit(a, b->digits[j], &R);
    shift_left(&R, WIDTH-1-j);
    add(r, &R, r);
  }

  return 0;
}