Implementing Basic Arithmetic for Large Integers: Multiplication: Karatsuba Multiplication Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Karatsuba Multiplication Algorithm

Now we will discuss one more algorithm for multiplication. We ﬁrst consider the case when the two operands have same number of digits. Say, the two operands are a = (a_n−1a_n−2…a₁a₀) and b = (b_n−1b_n−2…b₁b₀), each having n digits in base B, where n is even. We can break each of these numbers into two components as below, where k = n∕2:

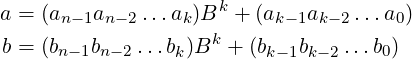
a = (a a ...a )Bk + (a a ...a ) n−1 n−2 k k k−1 k− 2 0 b = (bn−1bn−2...bk)B + (bk− 1bk− 2...b0)

We can denote these components as integers L_a, R_a, L_b, R_b (each having k-digits) and write:

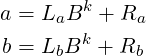
k a = LaB + Ra b = LbBk + Rb

The L and R symbols signify “Left” and “Right” half in the digit sequence. Now, the product of a and b can be expressed as:

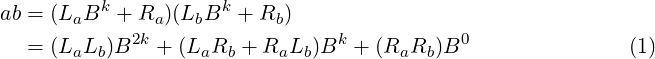
ab = (LaBk + Ra)(LbBk + Rb ) 2k k 0 = (LaLb )B + (LaRb + RaLb)B + (RaRb )B (1)

So, to obtain ab, one way is to ﬁrst compute each of (L_aL_b), (L_aR_b), (R_aL_b) and (R_aR_b) and use them in above expression. Each of these 4 terms require multiplication of two k-digit numbers. Note that multiplication by B^2k and B^k can be simply done by left-shifting by 2k and k positions respectively. The problem of multiplying a and b has been reduced to the subproblems of these 4 multiplications, followed by left-shifts and additions. This is in fact a Divide and Conquer approach.

Karatsuba Multiplication Algorithm (also described in [2] by its inventor A. A. Karatsuba) is based on the observation that the term (L_aR_b + R_aL_b) can be rewritten to give us something useful:

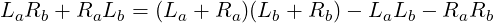L R + R L = (L + R )(L + R ) − L L − R R a b a b a a b b a b a b

(2)

Since L_aL_b and R_aR_b anyway need to be computed in (1), so just by doing one more multiplication (L_a + R_a)(L_b + R_b), we can avoid doing the two multiplications L_aR_b and R_aL_b.

Since adding two k-digit numbers may produce a (k + 1)-digit number, so the multiplication (L_a + R_a)(L_b + R_b) may involve (k + 1)-digit operands. We will be referring to a multiplication of operands having x and y digits as “a (x,y)-digits multiplication”.

Thus we are now required to perform overall two (k,k)-digits (L_aL_b, R_aR_b) and one (k + 1,k + 1)-digits multiplications, instead of four (k,k)-digits multiplications appearing in (1). Though, for this saving some extra work is required, like additions (L_a + R_a) and (L_b + R_b), and subtractions of L_aL_b and R_aR_b as seen in (2).

This same technique can be recursively applied while solving the three multiplication subproblems. If number of digits (n) is not even for any subproblem, we can choose k = ⌈n∕2⌉.

Let us denote by T(n) the time-complexity of this algorithm for (n,n)-digits multiplication, where n is even. For this complexity analysis, we will treat the (k + 1,k + 1)-digits multiplication as having complexity T(k) + c₁k (for some constant c₁), which is achievable. The extra work required for additions and subtractions in (2) can be written as c₂n for some constant c₂. So the recurrence relation for T(n) is, for some constant c:

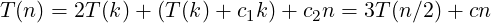T (n ) = 2T (k)+ (T(k) + c1k)+ c2n = 3T(n∕2 )+ cn

If we assume n to be a power of 2, T(n) will come out to be O(n^{log ₂3}). It is easy to see that the schoolbook multiplication algorithm has time-complexity O(n²) for (n,n)-digits multiplication.

[Prev] [Up] [Next]