Implementing Basic Arithmetic for Large Integers: Multiplication: Operands with Unequal Lengths

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Operands with Unequal Lengths

In above, we have assumed a and b to be having the same number of digits. Now, let us say, a has n_a digits and b has n_b digits, n_a ≥ n_b. For their multiplication, how can we beneﬁt from the above method?

Due to the Division Theorem, there must exist integers q, r with q ≥ 1, 0 ≤ r ≤ n_b − 1, such that:

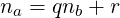n = qn + r a b

Starting from the least-signiﬁcant-digit (LSD) of a, we can divide it into q chunks of n_b digits each, and one last chunk of r digits which begins at the most-signiﬁcant-digit (MSD) of a. We can write a in terms of these chunks (components) as:

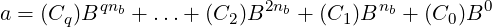a = (Cq)Bqnb + ...+ (C2)B2nb + (C1 )Bnb + (C0 )B0

where C₀,C₁,…,C_q−1 have n_b digits each and C_q has r digits. Note that, because of some 0 digits within a, these chunks may have redundant 0s at the beginning positions (starting at their MSD).

The product ab will be computed as:

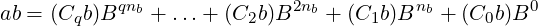qn 2n n 0 ab = (Cqb)B b + ...+ (C2b )B b + (C1b)B b + (C0b)B

That is, we will multiply each component with b, left-shift the results as required, and add them all. Note that, there are q multiplication subproblems of (n_b,n_b)-digits each, and 1 subproblem of (r,n_b)-digits. These subproblems can be recursively solved in the same manner; the earlier described Karatsuba method will be used whenever the two operands have equal number of digits.

[Prev] [Up] [Next]