[This page is auto-generated; please prefer to read the article’s PDF Form.]
Given any positive real number a, we want to find its logarithm in base 2, i.e. log 2a. In this article, whenever we specify “log”, it will mean log 2. Say, log a = n + f, where n is an integer and f is a fraction with 0 ≤ f < 1. That is, a = 2n+f = 2n2f, where 1 ≤ 2f < 2. Note that n is negative when a < 1. Also, 2n ≤ a < 2n+1 for all a.
In this article, we will often refer to the binary representation of some non-negative real number r, denoted as: (rmrm−1…r0.r−1r−2…)2. The bit ri is said to be at position i. rm is the most-significant-bit (MSB). The radix-point (.) separates the integer and fractional part of r. The value of r is given by:
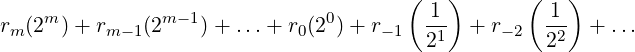 |
For example, in (110.101)2, (110)2 represents 6 and (0.101)2 represents 5∕8 = 0.625, giving the complete value of 6.625 in decimal.
If a is an integer and stored as an integer type, we can check the position of its MSB in the binary form. This bit position gives us the value of n. If a is a real number stored as a floating-point of IEEE standard 754 (significand × 2exponent), again we can exploit the storage format to find n.
If we do not want to depend upon the storage format of a, we can find n by other methods too. For example, if a ≥ 2, we can iteratively divide it by 2 until a < 2, while counting the number of divisions needed (the count is n). Similarly, if a < 1, we can iteratively multiply it by 2 until a ≥ 1 (the count is (−n)). There can be other more efficient methods also.
We now come to the problem of finding f. Once we know n, we will divide a by 2n to give us another real number x = a∕2n = 2f, where 1 ≤ x < 2. We need to find f = log x. There are a few algorithms known for this, and this operation is sometimes also provided by the hardware itself. We will discuss a simple algorithm which is based on very basic mathematics. It finds f iteratively one bit at a time.
[Next]
Copyright © 2021 Nitin Verma. All rights reserved.