Computing Logarithm Bit-by-Bit: Bit-by-Bit Algorithm

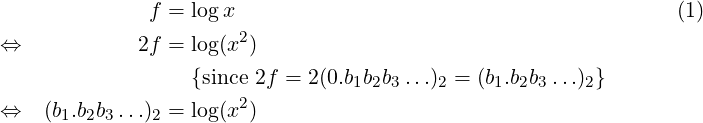
[This page is auto-generated; please prefer to read the article’s PDF Form.]

Bit-by-Bit Algorithm

The algorithm may have been discovered multiple times independently, but appears to be ﬁrst published in 1956 by D. R. Morrison [1]. Morrison provided a generic algorithm to ﬁnd inverse of any function which meets certain conditions, 2^y being one such function. Note, log ₂(2^y) = y, so the inverse of 2^y is the log ₂ function.

Since 0 ≤ f < 1, it can be written in binary form as: (0.b₁b₂b₃…)₂, where each b_i is a bit (0 or 1) at position (−i). The algorithm makes use of the below observations:

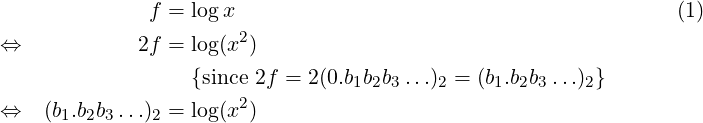
So, x² ≥ 2 implies b₁ must be 1, and x² < 2 implies b₁ must be 0. Thus, b₁ can be deduced just by comparing x² with 2. Further,

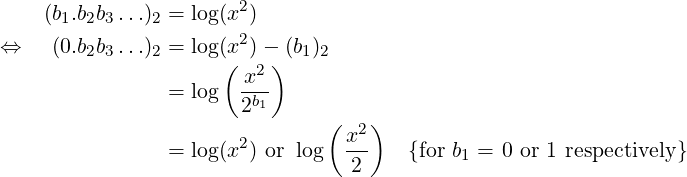
If we now consider (0.b₂b₃…)₂ to be our new f, and x² or x²∕2 (based on b₁) to be our new x, then above relation translates to f = log x, which is same as (1). Thus, bit b₂ can be found by the same process we used to ﬁnd b₁. Repeating this process m times will give us m bits of f up to b_m, which we can combine to give us an approximation for f as (0.b₁b₂b₃…b_m)₂.

Below is an implementation of this algorithm in C. Input x is assumed to follow 1 ≤ x < 2. m speciﬁes the number of bits to generate for f.

/* base-2 log bit-by-bit */
float log2_bbb(float x, int m)
{
  int i, bits, bit;

  if(x == 1)
    return 0;

  i = 0;
  bits = 0;

  /* loop-invariants:
       P: f = log(x) (variable f is unknown and shown commented)
       Q: 1 <= x < 2
       R: ’bits’ contains i bits appended as ’bit’ */

  while(i < m)
  {
    /* f <-- 2 * f */    /* maintain P */
    x = x * x;

    if(x >= 2)
    {
      bit = 1;
      /* f <-- f - 1 */    /* maintain P */
      x = x/2;
    }
    else
      bit = 0;

    bits = (bits << 1) | bit;

    i++;
  }

  /* ’bits’ contains m bits from f, so f =(approx) bits/(2^m) */

  return ((float)bits) / (1 << m);
}

There can be other variants of this algorithm. For example, we can write it for computing logarithm in any base b (log _bx). For that, the comparison x² ≥ 2 needs to be replaced by x² ≥ b to deduce the bit. And for the new x, division x²∕2 needs to be replaced by x²∕b.

Another variant is to treat f in any other radix d as (0.d₁d₂d₃…)_d, where each d_i is a digit in radix d. Then, instead of generating f one bit at a time, we can generate it one (radix-d) digit at a time. For that, both sides of (1) are multiplied by d, and instead of x² we need to compute x^d. Then, we need to ﬁnd digit d₁ such that 2^d₁ ≤ x^d < 2^d₁+1. After ﬁnding d₁, we will compute x^d∕2^d₁ instead of x²∕2^b₁ for our new x.