Cycle Detection: Brent’s Algorithm: The Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

The Algorithm

First we observe that, there must exist integer r such that e_r belongs to the cycle and e_r equals at least one element among its next r elements (e_r+1,e_r+2,…,e_r+r). Speciﬁcally, any integer r satisﬁes this condition if and only if:

So, for any given l and n, all integers max(l,n) onwards satisfy the criteria for r. The Brent’s algorithm attempts to ﬁnd r which is the minimum power of 2, 2^p (p is a non-negative integer), such that 2^p ≥ max(l,n). Now onwards, we will use r to denote this speciﬁc integer 2^p.

By ﬁnding r and locating e_r, the algorithm will have located some element in the cycle (since e_r belongs to the cycle), and will then proceed to ﬁnd l and n.

The algorithm works as follows. It sequentially checks if the candidates r′ = 2⁰,2¹,2²,…, satisfy the criteria for the desired r. That is, whether e_r′ equals any of its next r′ elements or not. To do that, it maintains two references M (mark) and R. For each r′, M is kept at e_r′ while R steps through the next r′ elements comparing them with M (e_r′). Note that this stepping of R will ﬁnally bring it at e_r′+r′ = e_2r′. So, for checking the next candidate r′, which is 2r′, this reference R at e_2r′ can be used to set the mark M for that next candidate.

Note that a candidate r′ does not satisfy the criteria if, either (a) e_r′ is outside the cycle (r′ < l), or (b) e_r′ is inside the cycle but is distinct from its next r′ elements (r′ < n).

Following is an implementation of this algorithm in C. The above described part of this method will be referred as “Cycle-Searching” (the other part “Find l” will be discussed below). Whenever a reference, say R, is updated to f(R), we will call it one “step” taken by R.

Note that when the desired r is reached, the value of n can be found by counting the steps R has taken after e_r to reach the nearest element equaling e_r.

/* Parameter f is a function pointer.
   Output values of n and l are returned via pointers pn and pl.

   The elements e{i} are referred using type "void *". So,
   function f has input and output type as "void *". */

void brent(void *e0, void* f(void*), int *pn, int *pl)
{
  void *R, *M, *R0;
  int i, r, cycle_found, count, j, n, l;

  /***** Cycle-Searching *****/

  /* initializations for the loop below */
  M = f(e0);
  r = 1;
  R = f(M);
  i = 2;
  cycle_found = (R == M);

  /* outer-loop invariants:

       1. M = e{r}

       2. R = e{i}

       3. (cycle_found AND (i = r + n) AND (R = M)) OR
          (!cycle_found AND (i = 2r)) */

  while(!cycle_found)
  {
    r = 2*r;

    M = R;

    /* Now, M = R = e{r}. R will take (upto) r steps till e{2r} */

    /* inner-loop invariant: R = e{i} */

    while(i < 2*r && !cycle_found)
    {
      R = f(R);
      i = i + 1;
      cycle_found = (R == M);
    }
  }

  n = i - r;

  /***** Find l *****/

  /* (M = e{r}) holds */

  if(r%n != 0)
  {
    j = r + n - r%n;
    i = r;

    while(i < j)
    {
      M = f(M);
      i = i + 1;
    }

    /* (M = e{j}) holds */
  }

  /* (M = e{multiple-of-n}) holds */
  R0 = e0;
  count = 0;

  while(R0 != M)
  {
    R0 = f(R0);
    M = f(M);
    count++;
  }

  /* (R0 = M = e{l}) holds */

  l = count;

  *pn = n;
  *pl = l;
}

This algorithm ﬁnds minimum power of 2, r = 2^p, such that 2^p ≥ max(l,n). Since 2^p is the minimum possible, we must have 2^p−1 < max(l,n), which can also be written as 2^p < 2 ⋅ max(l,n). So,

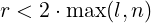Also, this algorithm (the cycle-searching part) steps R total r + n times. So, the number of calls to f performed by it is upper-bounded by: