Home

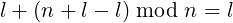
[This page is auto-generated; please prefer to read the article’s PDF Form.]

Finding l

We initialize two references R₀ and R_n at e₀ and e_n respectively. R_n can be placed at e_n by stepping n times from e₀. Now, after l steps, R₀ will be at index l and R_n will be at index (due to equation (1) in [1]):

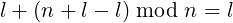So, to find l, we can iteratively step R₀ and R_n till they meet, while counting the steps. This step count will be l.

Alternatively, we can use another more efficient approach. When the cycle-searching loop terminates, M is at e_r. We will first place M at e_j, where j is a multiple of n. If n∣r, we are done with j = r. Otherwise, we use the fact that (r − r mod n), and hence (r + n − r mod n), is always a multiple of n. So, we step M (n − r mod n) times to bring it at e_j with j = (r + n − r mod n).

Now, initialize a reference R₀ at e₀. After l steps, it will be at index l. Also, M, which is at e_j, after l steps will be at index (due to equation (1) in [1]):

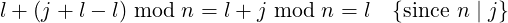So, to find l, we can iteratively step R₀ and M till they meet, while counting the steps. This step count will be l.

The “Find l” part in method brent() implements this approach.

The earlier approach steps R₀ and R_n l and n + l times respectively. This approach steps R₀ l times, but steps M l or (n − r mod n) + l times (based on n∣r or not). Note that, (n − r mod n) < n when n ∤ r.

■

References

[Prev]   [Up]   

Copyright © 2021 Nitin Verma. All rights reserved.