Generating Permutations with Recursion: Heap’s Algorithm

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Heap’s Algorithm

This algorithm is due to B. R. Heap [3]. Following is an implementation of this algorithm.

void brheap(int s)
{
  int i;

  if(s == N-1)
  {
    print();
    return;
  }

  for(i = 0; i < N-s; i++)
  {
    /* Setup Block */
    if(i > 0)
    {
      if((N-s)%2 != 0)
        SWAP(s, N-1)
      else
        SWAP(s, N-i)
    }

    brheap(s+1);
  }
}

Notice how the next element of B is picked based on whether N − s, the number of elements in subarray a[s : N − 1], is even or odd. What is most impressive about this algorithm is that it performs exactly one swap for each permutation generated (do we see why?). Thus it involves total N! − 1 swaps. This makes the algorithm one of the eﬃcient algorithms, because for moving from one permutation to any other, at least one swap is always required.

When executing this algorithm, we can notice that an invocation of this method for any s leaves the subarray a[s : N − 1] altered in a deﬁnite pattern (compare the subarray upon method entry and exit). This pattern only depends upon the parity of N − s, the number of elements in the subarray. Consider the subarray:

(e1 e2 e3 e4 e5 ... en− 1 en)

For odd n, we ﬁnd it becoming:

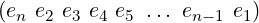(en e2 e3 e4 e5 ... en−1 e1)

For even n, we ﬁnd it becoming:

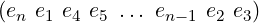(en e1 e4 e5 ... en−1 e2 e3)

The original paper [3] of this algorithm does not include a proof of correctness. D. E. Knuth in his book [4], asks to prove it as an exercise which hints at using the “Sims Table” (section “Generating All Permutations”, exercise 40). (I am still searching for an elegant proof of this algorithm and of the pattern observed above.)

[Prev] [Up] [Next]