Generating Permutations with Recursion: Intact-Rotate Algorithm

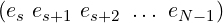
[This page is auto-generated; please prefer to read the article’s PDF Form.]

Intact-Rotate Algorithm

void intact(int s)
{
  int i;

  if(s == N-1)
  {
    print();
    return;
  }

  for(i = 0; i < N-s; i++)
  {
    rotate(s+1);

    SWAP(s, N-1);
  }
}

void rotate(int s)
{
  int i;

  if(s == N-1)
  {
    print();
    return;
  }

  for(i = 0; i < N-s; i++)
  {
    if(i > 0)
      SWAP(s, N-i);

    intact(s+1);
  }
}

Consider the iterations of intact(s). Assume that any call to rotate(s + 1) leaves the subarray a[s + 1 : N − 1] left-rotated by 1 place upon return. That is, if the subarray before the call is: (e_s+1 e_s+2 … e_N−1), it will become after the call: (e_s+2 e_s+3 … e_N−1 e_s+1).

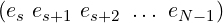Due to the call to rotate(s + 1) followed by the swap, the subarray will become, at the end of the iteration:

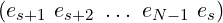This is nothing but a left-rotation of the subarray a[s : N − 1]. Thus the side-eﬀect of each iteration is to left-rotate a[s : N − 1]. So the total of N − s such iterations will left-rotate this subarray (of N −s elements) by N −s places, leaving it what it was prior to the loop. So we can conclude that intact() leaves the subarray a[s : N − 1] intact upon return.

Now consider the iterations of rotate(s) and assume that any call to intact(s + 1) leaves the subarray a[s + 1 : N − 1] intact upon return. To see the side-eﬀect of the iterations, we can ignore the call to intact(s + 1) and simply consider the eﬀect of executing the swaps. We can ﬁgure out that when the loop terminates, the subarray a[s : N − 1] must have left-rotated by 1 place.

Also notice that the base-case (s = N − 1) of both the methods leaves the subarray a[N − 1 : N − 1] intact which can also be seen as a left-rotation of the single element subarray.

Suppose we associate a speciﬁcation to intact() and rotate() each that they leave the subarray a[s : N − 1] intact and left-rotated respectively upon return. In above paragraphs, we proved that intact() and rotate() follow their speciﬁcation assuming that their recursive call to the other one also follows its own speciﬁcation. As we saw, their base-case also follows the speciﬁcation. So, by applying Mathematical Induction over N − s, we can conclude that both methods do follow their speciﬁcation.

Now that we have established how a call to intact() and rotate() leaves the subarray upon return, it is easy to see why the swapping with index N − 1 and N − i by these methods will pick all elements of B correctly. In conclusion, invoking any of these two methods with s = 0 must generate all permutations of array a.

We can notice some similarity among these two methods and the brheap() shown earlier: each of them involves N −s iterations where almost all iterations perform one swap each. The iterations of intact() do total N −s swaps but those of rotate() and brheap() do total N − s − 1 swaps. Thus there is one extra swap for each invocation of intact(), making this algorithm less eﬃcient than the Heap’s Algorithm.

Since the two methods call each other, any execution of this algorithm must involve their alternate invocations: one particular method for even s and the other one for odd s. Also, the structure of these methods are similar. So we can combine these into a single method as below, which adheres to the common recursive structure:

void intact_rotate(int s)
{
  int i;

  if(s == N-1)
  {
    print();
    return;
  }

  for(i = 0; i < N-s; i++)
  {
    /* Setup Block (for rotate()) */
    if(i > 0 && ((N-s)%2 == 0))
      SWAP(s, N-i);

    intact_rotate(s+1);

    /* Cleanup Block (for intact()) */
    if((N-s)%2 != 0)
      SWAP(s, N-1);
  }
}