Some Proofs About Fibonacci Numbers: Relation 1

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Relation 1

Since F_n+1 = F_n−1 + F_n, so if we take product F_n ⋅F_n+1, the outcome will again contain a similar and smaller product term: F_n−1 ⋅ F_n. We can attempt to repeat this process for subsequent smaller product terms. Assume n to be large enough to allow some iterations and observation of the repeating pattern.

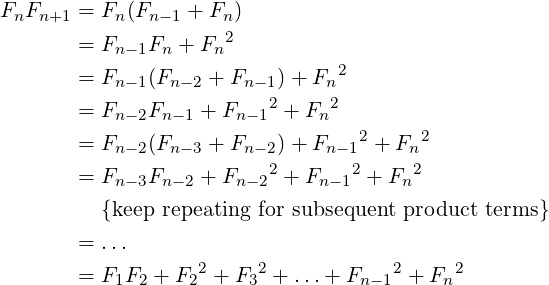
FnFn+1 = Fn (Fn−1 + Fn) = Fn −1Fn + Fn2 2 = Fn −1(Fn−2 + Fn−1) + Fn = Fn −2Fn− 1 + Fn− 12 + Fn2 = Fn −2(Fn−3 + Fn−2) + Fn−12 + Fn2 2 2 2 = Fn −3Fn− 2 + Fn− 2 + Fn−1 + Fn {keep repeating for subsequent product terms} = ... 2 2 2 2 = F1F2 + F2 + F3 + ...+ Fn−1 + Fn

Since F₁F₂ = 1, we can write below relation for all n ≥ 2:

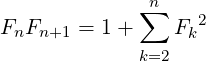∑n FnFn+1 = 1+ Fk2 k=2

(2)

Example: F₆F₇ = 8 ⋅ 13 = 104 = 1 + 1² + 2² + 3² + 5² + 8²

[Prev] [Up] [Next]