Comparing Performance of Insertion Sort and Selection Sort:Counting the Operations

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Counting the Operations

We will simply use “transfer” to refer to the copying of an object from one location to another, and “comparison” to refer to a less_than() call.

In insertion_sort(), the outer loop runs (n− 1) times. Since the inner loop can run anywhere between 0 to i times, for our analysis we assume it to run fi times for some f in interval [0,1]. Each iteration of the outer loop will do (fi + 2) transfers. Due to the inner loop, there will be (fi + 1) comparisons. So the total number of transfers and comparisons in the method will be respectively:

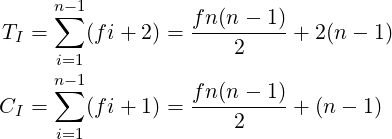
n−1 T = ∑ (fi+ 2) = f-n(n−-1) + 2(n − 1) I i=1 2 n−1 C = ∑ (fi+ 1) = f-n(n−-1) + (n − 1) I 2 i=1

For the case when the input array is already sorted, the inner loop will run 0 times, giving f = 0, and so T_I = 2(n− 1), C_I = (n− 1). Here the method has a linear time complexity in n. But when the input array is in decreasing order, the inner loop will run i times, giving f = 1, and so T_I = (n − 1)(n + 4)∕2, C_I = (n− 1)(n + 2)∕2. In this case, the method has a quadratic time complexity in n.

For our analysis below, we will assume f = 1∕2 (the element a[i] inserted in the middle of the sorted subarray), and so:

TI = (n-−-1)(n+--8) 4 CI = (n-−-1)(n+--4) (1) 4

In selection_sort() too, the outer loop runs (n− 1) times. But the inner loop always runs (n−i− 1) times. Each iteration of the outer loop will do (n−i− 1) comparisons (due to the inner loop) and 3 transfers (for swapping a[i] and a[min]). So the total number of transfers and comparisons in the method will be respectively:

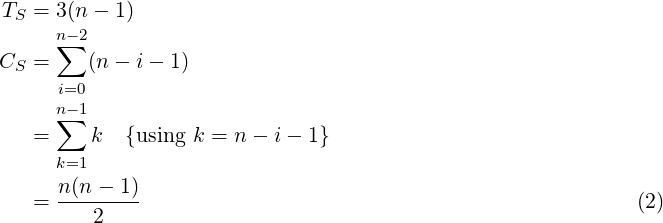
TS = 3(n − 1) n∑−2 CS = (n − i− 1) i=0 n∑−1 = k {using k = n − i− 1} k=1 n-(n-−-1) = 2 (2)

[Prev] [Up] [Next]