Home

[This page is auto-generated; please prefer to read the article’s PDF Form.]

First Estimate

Let us say, we first estimate the desired quotient-digit d to be the following based on the initial digits of the divisor b and IDD x:

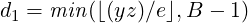(7)

Since d₁ ≤⌊(yz)∕e⌋,

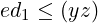(8)

Can this estimate d₁ be less than d? Let’s assume the case when d₁ < d. Since d ≤ B − 1, we must have d₁ < B − 1, i.e. d₁ = ⌊(yz)∕e⌋. But that means,

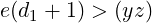In the multiplication bs{s = d₁ + 1} from the last section, the value (uv) in the result will follow, due to (3) and above:

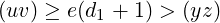Thus, b(d₁ + 1) would exceed the IDD x (using (5)), and so d₁ + 1 or any higher digit cannot be the desired quotient-digit d. This contradicts our assumption that d₁ < d. Hence,

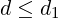(9)

[Prev]   [Up]   [Next]   

Copyright © 2021 Nitin Verma. All rights reserved.