[This page is auto-generated; please prefer to read the article’s PDF Form.]
Now we need to figure out, by how much d1 may exceed d. Note that in the multiplication bs{s = d1}, the value (uv) in the result follows (due to (2)):
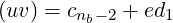 |
where carry cnb−2 cannot exceed (d1 − 1).
Due to (8), the ed1 term is less than or equal to (yz), and the contribution by the carry term may further lead to (uv) exceeding (yz). If that happens, we definitely know that bd1 > x (using (5)) and d1 is not the correct quotient-digit.
Intuitively, this contribution by carry term (up to (d1 − 1)), which is roughly bounded by B, can be counterbalanced by reducing d1 to d1 − Δ in the ed1 term, for some Δ. Then, ed1 reduces by eΔ, and so we can be sure to counterbalance the contribution of B by this eΔ if eΔ ≥ B.
We can see, the larger is e, the lesser Δ is required to ensure this counterbalancing. Now we will look at this idea formally.
Copyright © 2021 Nitin Verma. All rights reserved.