Three Distance Theorem: Gap Lengths

[This page is auto-generated; please prefer to read the article’s PDF Form.]

[Prev] [Up] [Next]

Gap Lengths

For i = 1,2,…,N − 1, let us refer to the distance from {uiα} to {ui+1α} as gap-i. The distance from 0 to {u1α} can be referred as gap-0, and that from {uNα} to 1 can be referred as gap-N. Trivially, gap-0 and gap-N are {u1α} and 1 −{uNα} respectively.

Consider some gap-i such that ui lies in interval (b) of theorem 1. Then,

{ui+1α} = {(ui + u1 − uN )α} = {uiα + u1α − uN α} (from all the three real numbers inside {}, we can remove their integer part, and add 1 for the negative number ) = {{uiα} + {u1α} + 1 − {uNα }}

Say, f = {u1α} + 1 −{uNα}, which is the sum of gap-0 and gap-N. So, 0 < f ≤ 1. Then,

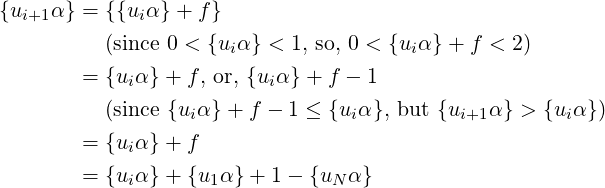
{ui+1α} = {{uiα} + f} (since 0 < {uiα} < 1, so, 0 < {uiα }+ f < 2) = {uiα} + f, or, {uiα}+ f − 1 (since {uiα} + f − 1 ≤ {uiα }, but {ui+1α} > {uiα}) = {uiα} + f = {uiα} + {u1α }+ 1 − {uNα }

Thus, in case when ui lies in interval (b), gap-i is {ui+1α}−{uiα} = {u1α}+1−{uNα}. Similarly, we can prove that when ui lies in intervals (a) or (c), gap-i is {u1α} and 1 −{uNα} respectively.

Note that uN, which corresponds to gap-N, also falls into the range of interval (c). Now we can conclude the following about all of the N + 1 gaps, including gap-0 and gap-N. We count the number of ui integers in each of the three intervals.

Theorem 2. Among the total N+1 gaps, there are N+1−u1 gaps of length L₁ = {u1α}, N+1−uN gaps of length L₂ = 1−{uNα}, and uN +u1−(N+1) gaps of length L₁+L₂. The gaps of length L₁+L₂ exist iﬀ uN +u1 > N +1.

Can the gap-lengths L₁ and L₂ ever become equal? It can be proved that they will always be distinct for irrational α. Assuming they are equal:

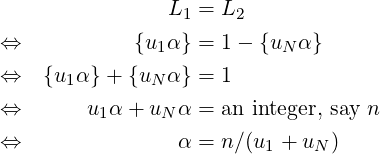
L = L 1 2 ⇔ {u1α } = 1− {uN α} ⇔ {u1α} + {uNα } = 1 ⇔ u1α + uN α = an integer, say n ⇔ α = n∕(u1 + uN )

But this would mean α is a rational number, a contradiction.

Corollary 3. For irrational α, the gap-lengths L₁ and L₂ are never equal. So, when gaps of length L₁ + L₂ exist, there are three distinct gap-lengths, otherwise two distinct gap-lengths.

We have seen how the length of all gaps are related to u1 and uN. The next section presents a theorem which relates u1 and uN to the Continued Fraction of α.

[Prev] [Up] [Next]