Home

[This page is auto-generated; please prefer to read the article’s PDF Form.]


[Prev]   [Up]   [Next]   

u1, uN and Continued Fraction of α

Theorem 4. For integer N ≥ 1, let t, r and s be the unique integers as defined by (3) and (4). Then,

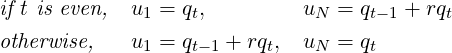
if t is even, u1 = qt, uN = qt−1 + rqt otherwise, u1 = qt−1 + rqt, uN = qt

Given α and N, we can use theorem 4 to find u1 and uN from the continued fraction of α and then use theorem 2 to find the gap-lengths.

Let us see an example of how the gap-lengths get created with α = 7∕23. Its simple continued fraction is: 7∕23 = 0 + 1∕(3 + 1∕(3 + 1∕2)) = [0;3,3,2].

So the convergents are: p0∕q0 = 0∕1,p1∕q1 = 1∕3,p2∕q2 = 3∕10,p3∕q3 = 7∕23.

The figure 2 below shows N = 8 and N = 11 points. The value {mα} is indicated with (m), m = 1,2,…,N. Since all values {mα} = {7m∕23} will be some multiples of 1/23, so in the figure we have also marked all multiples of 1/23 in [0,1].


Figure 2: α = 7∕23

PICT

Since q0 + q1 = 4 and q1 + q2 = 13, so for both N = 8 and N = 11, t = 1 based on (3). Using (4) with t = 1,

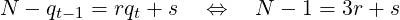N − q = rq + s ⇔ N − 1 = 3r + s t−1 t

So, for N = 8, r = 2 and s = 1. For N = 11, r = 3 and s = 1.

Using theorem 4, as t is odd, so for N = 8:

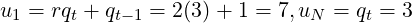u1 = rqt + qt−1 = 2(3) + 1 = 7,uN = qt = 3

and for N = 11:

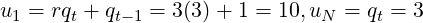u1 = rqt + qt−1 = 3(3) + 1 = 10,uN = qt = 3

So for both N, the gap-length L2 = 1 −{uNα} = 1 −{3(7∕23)} = 2∕23. For N = 8, gap-length L1 = {u1α} = {7(7∕23)} = 3∕23. For N = 11, gap-length L1 = {u1α} = {10(7∕23)} = 1∕23.

The gap-length L1 + L2, for N = 8 is 3∕23 + 2∕23 = 5∕23, and for N = 11 is 1∕23 + 2∕23 = 3∕23.

Using theorem 2, the counts of gap-length L1, L2 and L1 + L2 must respectively be: N + 1 − u1, N + 1 − uN and u1 + uN − (N + 1). For N = 8, these counts are: 2, 6 and 1. For N = 11, these counts are: 2, 9 and 1.

We see these same gap-lengths and their counts in the figure also.

We can also relate the existence of L1 + L2 gap-length with qt and s as below.

Corollary 5. The gap-length of L1 + L2 exists iff  s < qt − 1.

Proof. From theorem 2, gap-length of L1 + L2 exist iff  :

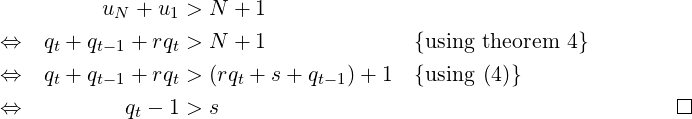
uN + u1 > N + 1 ⇔ qt + qt−1 + rqt > N + 1 {using theorem 4} ⇔ q + q + rq > (rq + s+ q )+ 1 {using (4)} t t−1 t t t−1 -| ⇔ qt − 1 > s --

As the range of s is 0 ≤ s ≤ qt − 1, so this gap-length does not exist when s = qt − 1.

In the above example with α = 7∕23, the gap-length L1 + L2 existed for both N because for both N, s = 1 and so qt − 1 = 2 > s.

[Prev]   [Up]   [Next]   

Copyright © 2020 Nitin Verma. All rights reserved.